三角形的外接圆（三角形的外接圆怎么画）

如何用圆规作等边三角形的外接圆和内切圆

1、用圆规作等边三角形的外接圆：如图，在等边三角形任意两边各作一条垂直平分线，两条垂直平分线的交点就是外接圆圆心，这时以该交点和三角形任意一角的连线为半径作圆，即为该三角形的外接圆。

2、不是内接圆，是内切圆 三角形内切圆的圆心是 三个角角平分线的交点。外接圆的圆心是三边的垂直平分线的交点。

3、问题一：怎么做三角形的外接圆？ 利用直尺和圆规做三角形其中两条边的垂直平分线，两条垂直平分线的交点就是三角形外接圆的圆心（叫做外心），再利用圆规，以交点为圆心，交点到三角形其中一个角的距离为半径画圆，就可以得到三角形的外接圆。

4、做三边的中垂线，他们的交点就是三角形外接圆的圆心了。

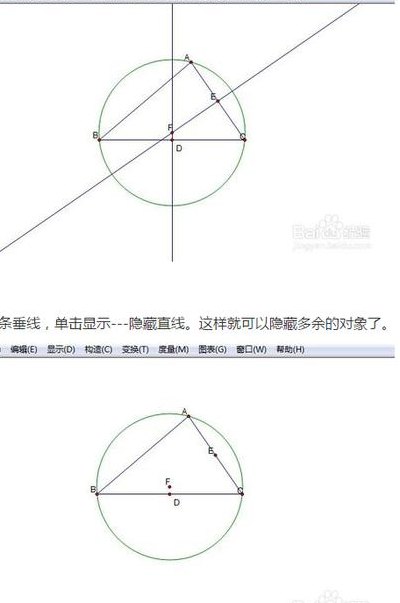
5、选择“线段直尺工具”，做出三角形ABC，具体如图所示。依次选择线段AB、线段BC，画出这两条边的中点D、E，具体如图所示。做线段AB、线段BC的垂直平分线，相交于O点，连接OE和DE，具体如图所示。以OB作为圆的半径，画出三角形的外接圆，具体如图所示。

6、几何画板的功能比较强大，可以取代数学中的三角尺和圆规。利用三角尺和圆规可以作出很多图形，以三角形的外接圆为例，下面介绍几何画板三角形外接圆的绘制方法：选择“线段直尺工具”，做出三角形ABC。依次选择线段AB、线段BC，执行“构造”—“中点”命令，在线段AB和线段BC分别出现中点D、E。

三角形外接圆是什么线的交点

三角形的外接圆的圆心是任意两边垂直平分线的交点。垂直平分线，经过某一条线段的中点，并且垂直于这条线段的直线，叫作这条线段的垂直平分线，又称“中垂线”，垂直平分线可以看成到线段两个端点距离相等的点的集合，垂直平分线是线段的一条对称轴。

三角形的外接圆圆心是任意两边垂直平分线的交点。三角形外接圆的性质 三角形外接圆的圆心是三角形外心，外心到三角形三个顶点的距离相等。三角形外接圆的半径是三角形外心到任意一个顶点的距离。三角形内心、垂心、重心和外心四个点共圆，即在三角形外接圆上。

三角形外接圆的圆心是三角形三条边的垂直平分线的交点。垂直平分线的交点这个点称为外心，是三角形外接圆的中心，即所有三角形顶点都位于该圆上的唯一圆，外心同时也是三角形的外接圆半径的中心，而三角形外接圆的圆心是三角形三条边的垂直平分线的交点。

三角形的外接圆圆心是任意两边的垂直平分线的交点，外接圆圆心叫外心。三角形有外接圆，其他的图形不一定有外接圆。轴对称图形的对称轴是对称图形中任意两个对应点连线段的垂直平分线。三角形三条边的垂直平分线以线段为例，可以看作是三角形一边。

三角形外接圆的圆心是三角形三条垂直平分线的交点。详细解释如下：三角形外接圆的圆心是通过研究三角形与其外接圆的关系得出的几何规律。对于任何一个三角形，都存在一个外接圆，并且这个外接圆有一个圆心。外接圆的圆心并不是随意确定的，而是根据三角形的特定性质来确定的。

三角形的外心是三遍垂直平分线的交点，它到三角形三个顶点的距离相等，三角形外接圆的圆心叫做三角形的外心。三角形外接圆的圆心也就是三角形三边垂直平分线的交点，三角形的三个顶点就在这个外接圆上。

外接圆和内切圆的定义?

1、外切圆：如果两个圆只有一个公共点，且圆心的距离等于两个圆半径的和，则这两个圆互为外切圆。两圆外切时，有3条公切线。内切圆：若一个二维平面上的多边形的每条边都能与其内部的一个圆形相切，该圆就是多边形的内切圆。

2、外接圆：与多边形各顶点都相交的圆叫做多边形的外接圆，通常是针对一个凸多边形来说的，如三角形，若一个圆恰好过三个顶点，这个圆就叫作三角形的外接圆，此时圆正好把三角形包围。

3、三角形的外接圆定理：（1）三角形各边垂直平分线的交点，是外心。（2）外心到三角形各顶点的距离相等。（3）外心到三角形各边的垂线平分各边。三角形的内切圆定理：（1）三角形各内角平分线的交点，是内心。（2）内心到三角形各边的距离相等。（3）三角形任一顶点到内切圆的两切线长相等。

4、外接圆：一个凸多边形的外接圆是指通过该多边形所有顶点的圆。这个圆不仅与多边形的边相交于点，而且每个交点都是圆上的点。例如，一个三角形的外接圆会恰好通过三个顶点，并且这个圆能够完全包含三角形。 内切圆：内切圆是指一个二维平面多边形的每条边都与该多边形内部的一个圆相切的圆。

5、与三角形三边都相切的圆叫做三角形的内切圆，圆心叫做三角形的内心，三角形叫做圆的外切三角形，三角形的内心是三角形三条角平分线的交点。与多边形各顶点都相交的圆叫做多边形的外接圆。三角形有外接圆，其他的图形不一定有外接圆。三角形的外接圆圆心是任意两边的垂直平分线的交点。

三角形外接圆公式

三角形外接圆的公式是：2R=a*b/(b-c)。三角形和外接圆的基本性质与公式推导 这个公式的基础是三角形的一些基本性质。三角形有外接圆，这个圆的直径等于三角形的最长边（我们假设是a），而它的半径等于三角形中最长的边的一半（即a/2）。

三角形的外接圆公式是a/sinA=b/sinB=c/sinC=2R，与多边形各顶点都相交的圆叫做多边形的外接圆，三角形有外接圆，其他的图形不一定有外接圆。三角形的外接圆圆心是任意两边的垂直平分线的交点。三角形外接圆圆心叫外心。

三角形外接圆面积公式：r=sqrt(s(s-a)(s-b)(s-c))其中，r是三角形外接圆的半径，s是这个三角形的半周长，a、b、c分别是这个三角具体公式如下：A=πr其中，A是这个圆的面积，r是这个圆的半径，π是圆周率。

外接圆半径R=a/sinA=b/sinB=c/sinC=2R。面积=πR方。外接圆的性质：锐角三角形的中心在三角形的内部。直角三角形的外中心在其斜边的中点。钝角三角形的外中心在三角形之外。具有外中心的图形必须有一个外圆（每侧垂直线的交点，称为外中心）。外接圆中心到三角形各顶点的线段长度相等。

三角形外接圆半径公式为：R = a / )。其中，R是外接圆的半径，a是三角形的边长，A是与边长a相对应的角的角度。这一公式常用于计算三角形的外接圆的半径。接下来将详细解释这个公式的含义和来源。三角形外接圆的概念 三角形外接圆是指一个圆完整地包含三角形的三个顶点。

设圆的一般方程为x^2+y^2+Dx+Ey+F=0。由该圆过已知三角形的三个顶点，将三个顶点坐标代入圆的一般方程。得到关于D，E，F的三元一次方程组，解得D，E，F即可。三角形任意两边的垂直平分线，两个垂直平分线的交点就是三角形外接圆的圆心。