全微分基本公式（三角函数中的万能公式）

全微分公式是什么?

1、函数\( z = f(x， y) \)的全微分公式描述了该函数在点\( (x， y) \)处，由于自变量\( x \)和\( y \)的增量\( \Delta x \)和\( \Delta y \)而引起的函数增量\( \Delta z \)的一个线性表达式。

2、函数z=f(x， y) 的两个偏导数fx(x， y)， fy(x， y)分别与自变量的增量△x， △y乘积之和fx(x， y)△x + fy(x， y)△y若该表达式与函数的全增量△z之差，当ρ→0时，是ρ( )的高阶无穷小，那么该表达式称为函数z=f(x， y) 在(x， y)处(关于△x， △y)的全微分。

3、求全微分dz公式：dz=tanα+cotα。微分在数学中的定义：由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。

4、结论：全微分公式是描述多元函数z=f(x， y)在某点(x， y)处，其变化量dz与自变量增量△x和△y的线性关系。当函数的全增量△z与偏导数fx(x， y)△x + fy(x， y)△y的差在ρ趋向于0时，如果这个差是ρ的高阶无穷小，那么这个表达式就被称为函数在该点的全微分。

5、例如，假设函数f(x)=x^2，那么在x=2的点，f(2)=4。因此，f(2+dx)-f(2)≈f(2)dx。这里，dx表示自变量x的微小变化。全微分公式为：df(a)=f(a)dx。其中，df(a)表示函数f在点a的全微分，f(a)表示f在点a的导数。当自变量发生微小变化时，函数值的变化可以用全微分来近似。

6、全微分公式推导的三个要点： 定义：对于二元函数z=f(x， y)，其在点(x， y)处的全微分表示为dz=AΔx + BΔy，其中A和B是函数在点(x， y)处的偏导数，且不依赖于Δx和Δy。

全微分的公式是什么?

函数z=f(x， y) 的两个偏导数fx(x， y)， fy(x， y)分别与自变量的增量△x， △y乘积之和fx(x， y)△x + fy(x， y)△y若该表达式与函数的全增量△z之差，当ρ→0时，是ρ( )的高阶无穷小，那么该表达式称为函数z=f(x， y) 在(x， y)处(关于△x， △y)的全微分。

求全微分dz公式：dz=tanα+cotα。微分在数学中的定义：由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。

函数\( z = f(x， y) \)的全微分公式描述了该函数在点\( (x， y) \)处，由于自变量\( x \)和\( y \)的增量\( \Delta x \)和\( \Delta y \)而引起的函数增量\( \Delta z \)的一个线性表达式。

结论：全微分公式是描述多元函数z=f(x， y)在某点(x， y)处，其变化量dz与自变量增量△x和△y的线性关系。当函数的全增量△z与偏导数fx(x， y)△x + fy(x， y)△y的差在ρ趋向于0时，如果这个差是ρ的高阶无穷小，那么这个表达式就被称为函数在该点的全微分。

全微分的公式

函数z=f(x， y) 的两个偏导数fx(x， y)， fy(x， y)分别与自变量的增量△x， △y乘积之和fx(x， y)△x + fy(x， y)△y若该表达式与函数的全增量△z之差，当ρ→0时，是ρ( )的高阶无穷小，那么该表达式称为函数z=f(x， y) 在(x， y)处(关于△x， △y)的全微分。

求全微分dz公式：dz=tanα+cotα。微分在数学中的定义：由函数B=f(A)，得到A、B两个数集，在A中当dx靠近自己时，函数在dx处的极限叫作函数在dx处的微分，微分的中心思想是无穷分割。微分是函数改变量的线性主要部分。

函数\( z = f(x， y) \)的全微分公式描述了该函数在点\( (x， y) \)处，由于自变量\( x \)和\( y \)的增量\( \Delta x \)和\( \Delta y \)而引起的函数增量\( \Delta z \)的一个线性表达式。

全微分公式推导的三个要点： 定义：对于二元函数z=f(x， y)，其在点(x， y)处的全微分表示为dz=AΔx + BΔy，其中A和B是函数在点(x， y)处的偏导数，且不依赖于Δx和Δy。

x， y)分别与自变量的增量△x， △y乘积之和 fx(x， y)△x + fy(x， y)△y 若该表达式与函数的全增量△z之差，当ρ→0时，是ρ( )的高阶无穷小，那么该表达式称为函数z=f(x， y) 在(x， y)处(关于△x， △y)的全微分。

结论：全微分公式是描述多元函数z=f(x， y)在某点(x， y)处，其变化量dz与自变量增量△x和△y的线性关系。当函数的全增量△z与偏导数fx(x， y)△x + fy(x， y)△y的差在ρ趋向于0时，如果这个差是ρ的高阶无穷小，那么这个表达式就被称为函数在该点的全微分。

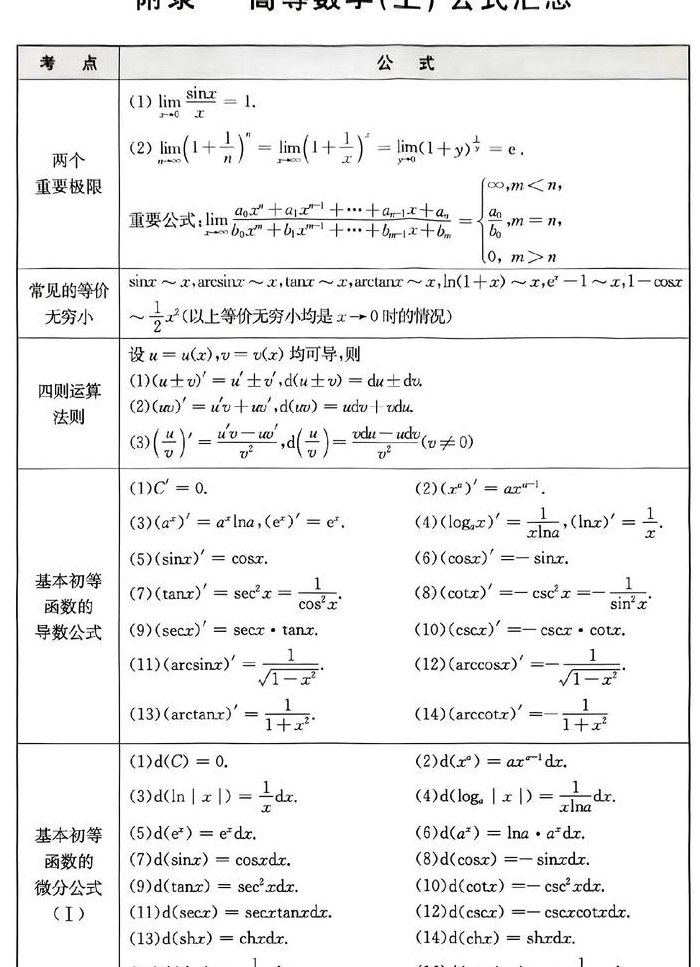
16个微分基本公式

对于常数C，其微分为0，即 d(C) = 0。 对于x的μ次方，其微分为μx^(μ-1)dx。 对于ax，其微分为axln(a)dx。 对于ex，其微分为exdx。 对于a的x次方，其微分为1/(xln(a))dx。 对于ln(x)，其微分为1/xdx。 对于sin(x)，其微分为cos(x)dx。

微积分基本公式共有16个，分别是常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数、双曲函数、反双曲函数的基本积分公式，以及换元积分法、分部积分法的公式。接下来，我将详细解释其中几个重要的公式。

基本微分公式：dy = f(x)dx。 微分公式的推导：设函数y = f(x)在某区间内定义良好，且x0及x0+△x在该区间内。

常用微分公式有： (1)d( C ) = 0 (C为常数)。 (2)d( xμ)=μxμ-1dx。 (3)d( ax ) = ax㏑adx。 (4)d( ex ) = exdx。 (5)d(㏒ax) = 1/(x*㏑a)dx。 (6)d(㏑x ) = 1/xdx。 (7)d( sin(x)) = cos(x)dx。

对数函数微分公式：对于自然对数函数f(x) = ln(x)或一般对数函数f(x) = log_a(x)（其中a为常数），其导数f(x) = 1/x或f(x) = 1/(x * lna)。例如，对于函数y = ln(x)，其导数为y = 1/x。对数函数在经济学、生物学等多个领域都有广泛应用。