0是不是有理数（310是不是有理数）

0是有理数还是无理数或者都不是?

1、综上所述，0是有理数，它不仅满足有理数的定义，而且在数学体系中占据着独特的位置，作为整数和分数的结合体，体现了有理数的广泛性和多样性。

2、有理数包不包括0：有理数包括0.有理数有：整数（正整数，负整数，0）分数（正分数，负分数）无理数：无限不循环小数。有理数是：整数(包括0，正负整数)，有限小数(如0.5)，无限循环小数(如1/3)，无理数是无限不循环小数(如圆周率和根号2)。

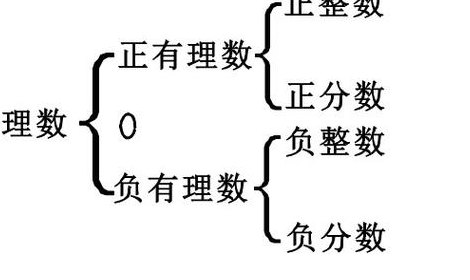
3、在数学中，0是一个特殊的存在，它既不属于正数也不属于负数，被称作中性数。有理数中包含了0，它们分为正有理数、0和负有理数三类。而无理数则仅有正负之分，0并不属于无理数的范畴。0的意义远不止表示“没有”，它在数学和实际生活中扮演着重要角色。

4、是有理数，不是无理数，无理数也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环，所以0是有理数。常见的无理数有非完全平方数的平方根、π和e，无理数的另一特征是无限的连分数表达式。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。

5、被归类为有理数，而非无理数。无理数定义为无限不循环的小数，如开方开不尽的数，例如根号2，以及像sin10度，sin20度等非明显无限不循环的小数，均属此类。而0作为整数，被归类为有理数，因为有理数包括有限小数和无限循环小数，整数本身即为有限小数的一部分，因此0自然属于有理数范畴。

0是有理数还是无理数或者都不是

1、综上所述，0是有理数，它不仅满足有理数的定义，而且在数学体系中占据着独特的位置，作为整数和分数的结合体，体现了有理数的广泛性和多样性。

2、在数学中，0是一个特殊的存在，它既不属于正数也不属于负数，被称作中性数。有理数中包含了0，它们分为正有理数、0和负有理数三类。而无理数则仅有正负之分，0并不属于无理数的范畴。0的意义远不止表示“没有”，它在数学和实际生活中扮演着重要角色。

3、是有理数，不是无理数，无理数也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环，所以0是有理数。常见的无理数有非完全平方数的平方根、π和e，无理数的另一特征是无限的连分数表达式。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。

4、探讨数系的构成，0的位置显得尤为特殊。作为数轴上的关键点，0既不归于正数范畴，也不属于负数序列，它独立于两端，构成了整数序列的一部分。在数学体系中，有理数与无理数是两个基本的分类。有理数包括整数、分数及它们的组合，而无理数则定义为不能表示为两个整数比例的数。

5、被归类为有理数，因为它可以被表示为两个整数的比值，即0/1。0并非无理数，因为无理数无法用两个整数的比值来表示。有理数包括自然数、偶数、整数和分数。自然数，即正整数，是整数的一部分，但整数不仅包括自然数，还有0和负整数。

6、是有理数，不是无理数。有理数是整数，和分数的统称，是整数和分数的集合。无理数的定义是无限不循环小数，而0是介于-1和1之间的整数，因此属于有理数。0是介于-1和1之间的整数，是最小的自然数，也是有理数。0不是正数，负数，质数，合数，0是自然数，而是正数和负数的分界点。

0是有理数还是无理数为什么

是有理数，不是无理数，无理数也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环，所以0是有理数。常见的无理数有非完全平方数的平方根、π和e，无理数的另一特征是无限的连分数表达式。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。

是有理数。0是介于-1和1之间的整数，既是最小的自然数，也是有理数；通常把能够写成分数形式的实数称为有理数，不是有理数的实数称为无理数。有理数的特征：有理数的小数部分是有限或为无限循环的数；无理数的特征：无理数的小数部分是无限不循环的数。

被归类为有理数，这源于数学中对有理数定义的深入探讨。在数学领域，有理数可以被描述为整数a与正整数b的比，即a/b形式。值得注意的是，0作为整数的一部分，自然地也属于有理数范畴，因为它可以表示为0/1的形式。有理数与无理数之间的区别不仅在于其定义，还在于它们的实质意义。