方差和期望的关系公式(方差和期望的关系公式推导)
期望与方差的关系怎样表示的
1、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。
2、方差=E(x)-E(x),E(X)是数学期望。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
3、对于随机变量X,其期望值用E(X)表示,方差用Var(X)表示。根据定义,方差和期望的关系可以通过以下公式表示:Var(X) = E((X - E(X))^2)这个公式表示方差等于随机变量X与其期望值E(X)之差的平方的期望值。
4、方差与期望的关系公式:DX=E(X^2-2XEX+(EX)^2)。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。概率,亦称“或然率”,它是反映随机事件出现的可能性(likelihood)大小。
方差和期望的关系公式是?
1、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。
2、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。
3、方差与期望的关系公式:DX=E(X^2-2XEX+(EX)^2)。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
数学期望和方差的公式是什么啊?
代入公式。在[a,b]上的均匀分布,期望=(a+b)/2,方差=[(b-a)^2]/2。代入直接得到结论。
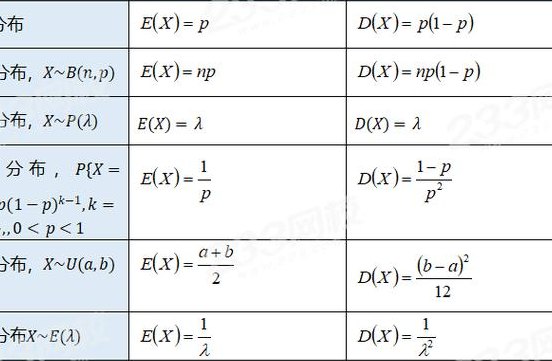
数学期望和方差公式为:EX=npDX=np(1-p)、EX=1/PDX=p^2/q、DX=E(X)^2-(EX)^2。对于2项分布(例子:在n次试验中有K次成功,每次成功概率为P,它的分布列求数学期望和方差)有EX=npDX=np(1-p)。
方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。
方程D(X)=E{[X-E(X)]^2}=E(X^2)-[ E(X)]^2,其中E(X)表示数学期望。对于连续型随机变量X。若其定义域为(a,b),概率密度函数为f(x),连续型随机变量X方差计算公式:D(X)=(x-μ)^2 f(x) dx。方差刻画了随机变量的取值对于其数学期望的离散程度。
期望值计算公式:E(X)=(n*M)/N [其中x是样本数,n为样本容量,M为样本总数,N为总体中的个体总数],求出均值,这就是超几何分布的数学期望值。
方程D(X)=E{[X-E(X)]^2}=E(X^2) - [ E(X)]^2,其中 E(X)表示数学期望。对于连续型随机变量X,若其定义域为(a,b),概率密度函数为f(x),连续型随机变量X方差计算公式:D(X)=(x-μ)^2 f(x) dx。
方差和期望的关系公式是什么?
方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。
方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。
方差与期望的关系公式:DX=E(X^2-2XEX+(EX)^2)。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
该公式是“Var(X)=E[(X?E(X))2]”。方差和期望的关系公式中E(X)表示随机变量X的期望(均值),E(X)2表示随机变量X平方后的期望值,(E(X))2是期望值的平方。这个公式表明,随机变量的方差是其平方期望与期望平方之间的差异,反映了随机变量偏离其期望值的程度。
方差和期望的转换公式
1、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。
2、期望与方差的转换公式是:方差DX等于随机变量X的平方的期望E(X^2)减去随机变量X的期望E(X)的平方。用数学符号表示就是:DX=E(X^2)-(E(X))^2。这个公式在概率论和数理统计中非常重要,它描述了随机变量与其数学期望之间的偏离程度,即方差是衡量随机变量离散程度的度量。
3、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。
方差与期望的关系公式是什么?
1、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。E(X把)=E(1/n∑Xi)=1/nE(∑Xi)=1/n∑E(Xi)=(1/n)nμ=μ。
2、方差和期望的关系公式:DX=EX^2-(EX)^2。若随机变量X的分布函数F(x)可表示成一个非负可积函数f(x)的积分,则称X为连续性随机变量,f(x)称为X的概率密度函数(分布密度函数)。
3、方差与期望的关系公式:DX=E(X^2-2XEX+(EX)^2)。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
4、该公式是“Var(X)=E[(X?E(X))2]”。方差和期望的关系公式中E(X)表示随机变量X的期望(均值),E(X)2表示随机变量X平方后的期望值,(E(X))2是期望值的平方。这个公式表明,随机变量的方差是其平方期望与期望平方之间的差异,反映了随机变量偏离其期望值的程度。
5、方差=E(x)-E(x),E(X)是数学期望。在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和,是最基本的数学特征之一。它反映随机变量平均取值的大小。
6、数学期望和方差公式为:EX=npDX=np(1-p)、EX=1/PDX=p^2/q、DX=E(X)^2-(EX)^2。对于2项分布(例子:在n次试验中有K次成功,每次成功概率为P,它的分布列求数学期望和方差)有EX=npDX=np(1-p)。