数学集合符号及含义（数学集合符号及含义常用集合）

数学集合中的所有符号及其意义?

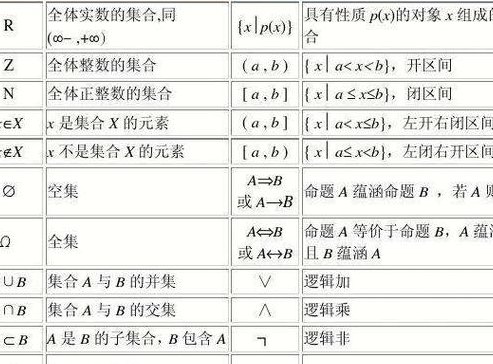
1、集合符号是数学中常用的符号之一，用于表示集合的概念。在数学中集合是由一些元素组成的整体，这些元素可以是数字、字母、符号等等。集合符号的使用可以让我们更加清晰地表达集合的概念 下面是一些常见的集合符号及其含义 0：大括号表示集合的符号，例如{1，2，3)表示由元素3组成的集合。

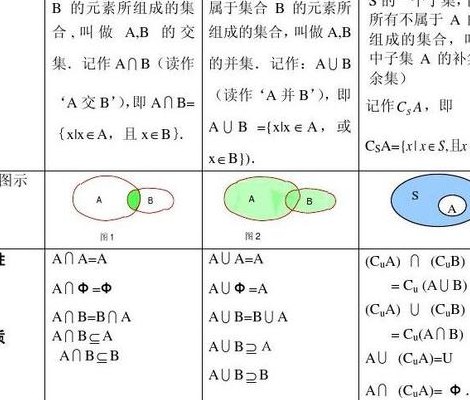
2、∪：并集，表示两个或多个集合合并后的所有元素。∩：交集，表示两个或多个集合共有的元素。∈：属于，表示元素属于某个集合。{…，…}：由元素a，b，c等构成的集合。[，]：表示实数集中的闭区间，例如[0， 1]表示从0到1（包括0和1）的所有实数。

3、∪ 表示集合的并集，即A∪B包含了集合A和集合B中的所有元素。∩ 表示集合的交集，即A∩B包含了同时属于集合A和集合B的所有元素。 表示子集，如果AB，则集合A是集合B的子集，意味着集合A中的所有元素都属于集合B。

4、数学集合的符号包括： 大括号{}：表示集合的所有元素。 冒号：表示“是...的集合”，例如{ x ： x 是自然数}表示自然数集合。 空集符号？：表示不含任何元素的集合，也称为空集。 子集符号？：表示集合A的所有元素都属于集合B，可以包含相同元素。

数学集合的符号有哪些?

1、数学集合的符号包括： 大括号{}：表示集合的所有元素。 冒号：表示“是...的集合”，例如{ x ： x 是自然数}表示自然数集合。 空集符号？：表示不含任何元素的集合，也称为空集。 子集符号？：表示集合A的所有元素都属于集合B，可以包含相同元素。

2、Q：代表有理数集合，由整数比上整数得到，包括所有分数和整数。 Q+：指正有理数集合，包含所有正分数和正整数。 Q-：表示负有理数集合，包括所有负分数和负整数。 R：表示实数集合，涵盖了所有有理数和无理数，是实数线的全体点。 R+：指正实数集合，包括所有正数。

3、Z：整数集合{…，-1，0，1，…}。Q：有理数集合。Q+：正有理数集合。Q-：负有理数集合。R：实数集合(包括有理数和无理数）。R+：正实数集合。R-：负实数集合。C：复数集合。1 ：空集（不含有任何元素的集合）。

4、数学集合符号如下：N：非负整数集合或自然数集合{0，1，2，3，…}。N*或N+：正整数集合{1，2，3，…}。Z：整数集合{…，-1，0，1，…}。Q：有理数集合。Q+：正有理数集合。Q-：负有理数集合。R：实数集合(包括有理数和无理数）。R+：正实数集合。

5、数学集合符号都有：N、N+、Z、Q、R、C等。具体介绍如下：全体非负整数的集合通常简称非负整数集（或自然数集），记作N。非负整数集内排除0的集，也称正整数集，记作N+（或N*）。全体整数的集合通常称作整数集，记作Z。全体有理数的集合通常简称有理数集，记作Q。

6、数学集合的符号主要包括以下几种： 集合的基本符号：如大括号{}，用于表示集合本身；竖线|，用于分隔集合中的元素；逗号，，用于分隔集合中的多个元素。

数学中集合字母的含义是指什么?

1、数学集合是指具有某种特定属性的事物的总体。集合论是数学中研究集合的分支，它研究了集合的性质、关系、运算以及集合之间的映射等。在数学中，集合通常用大写字母表示，且成员间没有重复。集合的成员可以是有限个数，也可以是无限个数。

2、Q：有理数集合。Q+：正有理数集合。Q-：负有理数集合。R：实数集合(包括有理数和无理数）。整数 整数，是序列{...，-3，-2，-1，0，1，2，3，...}中所有的数的统称，包括负整数、零（0）与正整数。和自然数一样，整数也是一个可数的无限集合。

3、数学中，N代表全体非负整数组成的集合，Z是整数集，Q是有理数集，R是实数集，C代表复数集合。N 全体非负整数的集合通常简称非负整数集，记作N。

4、 ：空集（不含有任何元素的集合）。集合基础知识：集合(简称集)是数学中一个基本概念，由康托尔提出。它是集合论的研究对象，集合论的基本理论直到19世纪才被创立。最简单的说法，即是在最原始的集合论--朴素集合论中的定义，集合就是一堆东西。集合里的东西，叫作元素。

5、N全体非负整数(或自然数）组成的集合；R是实数集；Z是整数集；Q是有理数集；Z*是正整数集；N*是正整数集。集合及运算的概念 集合：一般的，一定范围内某些确定的，不同的对象的全体构成一个集合。

数学集合符号及含义

1、集合符号的含义如下：含义 ∪：并集，表示两个或多个集合合并后的所有元素。∩：交集，表示两个或多个集合共有的元素。∈：属于，表示元素属于某个集合。{…，…}：由元素a，b，c等构成的集合。

2、下面是一些常见的集合符号及其含义 0：大括号表示集合的符号，例如{1，2，3)表示由元素3组成的集合。：空集符号，表示一个不包含任何元素的集合 ：属于符号，表示某个元素属于某个集合，例如aa，b，c表示元素a属于集合fa，b，c)。

3、数学集合的符号包括： 大括号{}：表示集合的所有元素。 冒号：表示“是...的集合”，例如{ x ： x 是自然数}表示自然数集合。 空集符号？：表示不含任何元素的集合，也称为空集。 子集符号？：表示集合A的所有元素都属于集合B，可以包含相同元素。

4、集合：用大写字母表示，如A、B、C等。元素：集合中的每一个对象称为元素，用小写字母表示，如a、b、c等。空集：不包含任何元素的集合，用符号_表示。全集：包含所有可能元素的集合，通常用符号U或R表示。

5、数学集合符号有N、N+、Z、Q、R、C等。全体非负整数的集合通常简称非负整数集（或自然数集），记作N。非负整数集内排除0的集，也称正整数集，记作N+（或N*）。全体整数的集合通常称作整数集，记作Z。全体有理数的集合通常简称有理数集，记作Q。

集合里面的符号及其含义

1、∪：并集，表示两个或多个集合合并后的所有元素。∩：交集，表示两个或多个集合共有的元素。∈：属于，表示元素属于某个集合。{…，…}：由元素a，b，c等构成的集合。[，]：表示实数集中的闭区间，例如[0， 1]表示从0到1（包括0和1）的所有实数。

2、：空集符号，表示一个不包含任何元素的集合 ：属于符号，表示某个元素属于某个集合，例如aa，b，c表示元素a属于集合fa，b，c)。：不属于符号，表示某个元素不属于某个集合，例如dea，b，c表示元素d不属于集合fa，b，c)。

3、集合：用大写字母表示，如A、B、C等。元素：集合中的每一个对象称为元素，用小写字母表示，如a、b、c等。空集：不包含任何元素的集合，用符号_表示。全集：包含所有可能元素的集合，通常用符号U或R表示。

4、集合的符号表示及意义如下：数学集合符号有N、N+、Z、Q、R、C等。全体非负整数的集合通常简称非负整数集（或自然数集），记作N。非负整数集内排除0的集，也称正整数集，记作N+（或N*）。全体整数的集合通常称作整数集，记作Z。全体有理数的集合通常简称有理数集，记作Q。

5、数学集合符号及含义如下：数学集合的定义 数学集合是指具有某种特定属性的事物的总体。集合论是数学中研究集合的分支，它研究了集合的性质、关系、运算以及集合之间的映射等。在数学中，集合通常用大写字母表示，且成员间没有重复。集合的成员可以是有限个数，也可以是无限个数。

集合里面的符号及其含义有哪些?

1、集合符号的含义如下：含义 ∪：并集，表示两个或多个集合合并后的所有元素。∩：交集，表示两个或多个集合共有的元素。∈：属于，表示元素属于某个集合。{…，…}：由元素a，b，c等构成的集合。

2、：空集符号，表示一个不包含任何元素的集合 ：属于符号，表示某个元素属于某个集合，例如aa，b，c表示元素a属于集合fa，b，c)。：不属于符号，表示某个元素不属于某个集合，例如dea，b，c表示元素d不属于集合fa，b，c)。

3、并集：两个或多个集合中所有元素的集合，用符号∪表示。交集：两个或多个集合中共有的元素的集合，用符号∩表示。补集：一个集合中不属于另一个集合的所有元素的集合，用符号-表示。笛卡尔积：两个集合中所有可能的有序对组成的集合，用符号×表示。