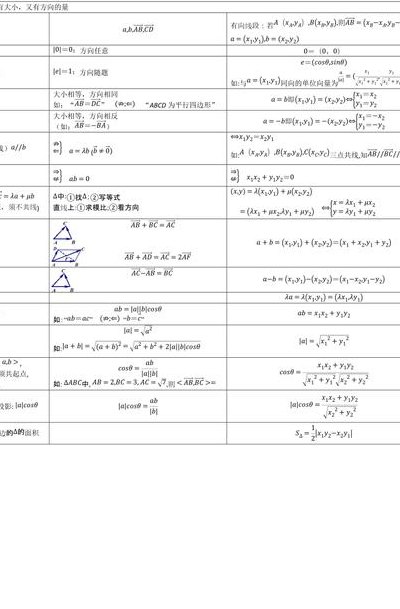
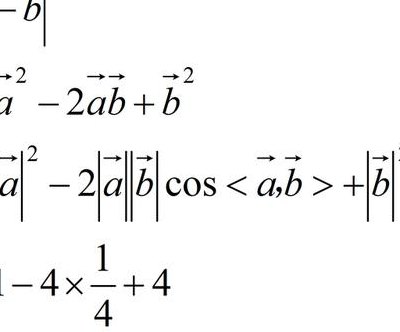模长公式(AB向量的模长公式)
两点模长的计算公式
1、两点模长的计算公式是√x+y+z。向量的模的计算公式有空间向量模长是√x+y+z平面向量模长是√x+y。
2、求向量模长公式:d=√x+y。向量AB(AB上面有→)的长度,记作|AB|(AB上有→)或|a|(a上有→)。向量的模的运算没有专门的法则,一般都是通过余弦定理计算两个向量的和、差的模。向量的性质 向量的模的运算没有专门的法则,一般都是通过余弦定理计算两个向量的和、差的模。
3、模长公式是向量的横坐标的平方加上向量纵坐标的平方的和再开平方。模长是指向量的长度,只有大小数值,没有向量带有的方向性。模是实数,且恒大于等于0。向量的模的运算没有专门的法则,一般都是通过余弦定理计算两个向量的和、差的模。
4、它的几何意义是复平面上一点(a,b)到原点的距离。运算法则:| z1·z2| = |z1|·|zhiz2| ┃| z1|-| z2|┃≤| z1+z2|≤| z1|+| z2| | z1-z2| = | z1z2|,是复平面的两点间距离公式,由此几何意义可以推出复平面上的直线、圆、双曲线、椭圆的方程以及抛物线。
5、┃|z1|-|z2|┃≤|z1+z2|≤|z1|+|z2| |z1-z2|,是复平面的两点间距离公式,由此几何意义可以推出复平面上的直线、圆、双曲线、椭圆的方程以及抛物线。复数实际上就是实数和虚数的总和,简单地说,复数就是由两部分构成的,一部分叫作实数部分,一部分叫作虚数部分。
请问向量的模长和数量积公式各是什么?
1、平面向量的模长(也叫长度)是平面向量的重要特性之一,表示向量在平面上的长度。平面向量的模长公式为:AB=/(某2-某1)2+(y2-y1)2。其中,A(某1,y1)和B(某2,y2)表示向量AB的起点和终点坐标。平面向量的加法和诚法公式 平面向量的加法和减法公式是指两个向量相加或相减的规则。
2、向量的模长公式 向量的模长是指向量的长度,它可以用勾股定理求得。设向量a=(x,y),则a的模长为la=V(x+y3)。向量的加法公式 向量的加法是指将两个向量相加得到一个新的向量。设向量a=(x1,y1)和向量b=(x2,y2),则atb=(x1+X2,y1+y2)。
3、向量乘以向量通常指的是向量的数量积或点积。数量积是一个标量,其值等于两个向量的模长与它们之间夹角的余弦的乘积。数量积的公式表示为:AB = |A| |B| cos,其中A和B是向量,|A|和|B|分别是它们的模长,是它们之间的夹角。数量积具有一些重要的性质和应用。
向量的模长是怎么样的?
1、平面向量(x,y),模长是:根号下(x^2+y^2)。
2、向量的模的计算公式:空间向量模长是√x+y+z平面向量模长是√x+y。空间向量(x,y,z),其中x,y,z分别是三轴上的坐标,模长是:√x+y+z。平面向量(x,y),模长是:√x+y。
3、向量的模也被称为向量的长度或向量的大小。对于一个二维向量(x,y)或三维向量(x,y,z),可以使用以下公式来计算向量的模:|v|=√(x^2+y^2)(二维向量),|v|=√(x^2+y^2+z^2)(三维向量)。表示乘方运算是^,表示平方根运算是√。
4、向量是有大小有方向的量,而模长只有大小没有方向,向量a与a的模长不存在有本质的关系,因为这是两个不相同的概念,但是向量a决定a的模长,向量a越大,那么a的模长越大,即|a|=a^2=a的模长。
5、模长的计算公式:向量的模公式空间向量(x,y,z),其中x,y,z分别是三轴上的坐标,模长是:√x+y+z平面向量(x,y),模长是:√x+y。
6、模长是指向量的长度,只有大小数值,没有向量带有的方向性。模是实数,且恒大于等于0。向量可以用有向线段来表示。有向线段的长度表示向量的大小,向量的大小,也就是向量的长度。箭头所指的方向表示向量的方向。
模长公式是什么?
模长公式是向量的横坐标的平方加上向量纵坐标的平方的和再开平方。模长是指向量的长度,只有大小数值,没有向量带有的方向性。模是实数,且恒大于等于0。向量的模的运算没有专门的法则,一般都是通过余弦定理计算两个向量的和、差的模。
向量的模的计算公式:空间向量模长是√x+y+z平面向量模长是√x+y。模长是指向量的长度,只有大小数值,没有向量带有的方向性。模是实数,且恒大于等于0。向量可以用有向线段来表示。
向量的模的计算公式:空间向量模长是√x+y+z平面向量模长是√x+y。向量的模:向量的大小,也就是向量的长度(或称模)。向量a的模记作|a|。向量注意:1.向量的模是非负实数,向量的模是可以比较大小的。
模长的计算公式:向量的模公式空间向量(x,y,z),其中x,y,z分别是三轴上的坐标,模长是:√x+y+z平面向量(x,y),模长是:√x+y。
平面向量的模长(也叫长度)是平面向量的重要特性之一,表示向量在平面上的长度。平面向量的模长公式为:AB=/(某2-某1)2+(y2-y1)2。其中,A(某1,y1)和B(某2,y2)表示向量AB的起点和终点坐标。平面向量的加法和诚法公式 平面向量的加法和减法公式是指两个向量相加或相减的规则。