一个多边形的内角和怎么求（一个多边形的内角和等于它的外角和求这个多边形边数）

多边形的内角和怎么算计算公式

1、内角的和公式：（n－2）×180°(n大于等于3且n为整数），则多边形各内角度数为：（n － 2）×180°÷n。多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。在平面多边形中，边数相等的凸多边形和凹多边形内角和相等。但是空间多边形不适用。n边形内角和为（n-2)*180度。

2、多边形的内角和公式为(n-2)×180°(n大于等于3且n为整数)。本文中，我整理了相关知识，欢迎大家阅读。

3、多边形内角和公式为：内角和=180°×（n-2）。其中n是多边形的边数。知识扩展 多边形是一个基本的几何概念，指的是一个平面图形，它由直线段组成，且每条边都是直的。多边形的定义取决于它的顶点数，即组成多边形的边的数量。如果一个多边形的每个顶点都是两条边的交点，则称为简单多边形。

4、答案：多边形的内角和公式为 (n-2)×180°，其中n是多边形的边数。解释：这个公式是如何得出的呢？当我们把一个n边形划分成(n-2)个三角形时，每个三角形的内角和为 180°。因此，多边形的内角和就是 (n-2) 个三角形的内角和之和，即(n-2)×180°。

5、多边形内角和计算公式为：n边形的内角和=（n-2)*180°。多边形的概念：数学用语，由三条或三条以上的线段首尾顺次连接所组成的平面图形叫做多边形。按照不同的标准，多边形可以分为正多边形和非正多边形、凸多边形及凹多边形等。

多边形的内角和与外角和怎么算?

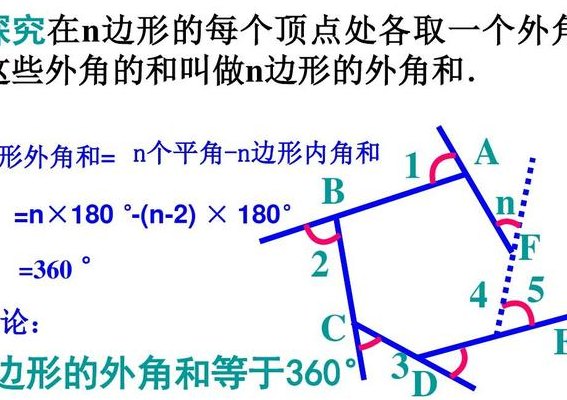
1、内角和：根据多边形内角和定理，N边形的内角和等于（N－2）×180°。外角和：相对的是外角，即从一个顶点出发的边延长后，与另一条边形成的夹角，内角与外角之和为180°。N边形的外角和总是等于360°。

2、多边形内角和公式：（n-2）×180°。多边形外角和公式：360 °。与多边形的内角相对应的是外角，多边形的外角就是将其中一条边延长并与另一条边相夹的那个角，任意凸多边形的外角和都为360°，多边形所有外角的和叫作多边形的外角和。

3、多边形的内角和公式：任意凸多边形的内角和为（n-2）×180°，其中n代表多边形的边数。这个公式是通过对多边形进行分割，将其转化为三角形来证明的，也可以通过归纳法得出，因为所有正多边形的内角和都符合这个规律。 多边形的外角和公式：任意凸多边形的外角和总是等于360°。

4、外角和计算公式 通常内角+外角=180度，所以每个外角中分别取一个相加，得到的和成为多边形的外角和。n边形的内角与外角的总和为n×180°，n边形的内角和为（n-2）×180°，那么n边形的外角和为360°。这就是说，多边形的外角和与边数无关。并且，三角形的一个外角等于不相邻的两个内角之和。

多边形内角和公式

内角的和公式：（n－2）×180°(n大于等于3且n为整数），则多边形各内角度数为：（n － 2）×180°÷n。多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。在平面多边形中，边数相等的凸多边形和凹多边形内角和相等。但是空间多边形不适用。n边形内角和为（n-2)*180度。

多边形的内角和公式为(n-2)×180°(n大于等于3且n为整数)。本文中，我整理了相关知识，欢迎大家阅读。

答案：多边形的内角和公式为 (n-2)×180°，其中n是多边形的边数。解释：这个公式是如何得出的呢？当我们把一个n边形划分成(n-2)个三角形时，每个三角形的内角和为 180°。因此，多边形的内角和就是 (n-2) 个三角形的内角和之和，即(n-2)×180°。

多边形边数公式：n边形的边=（内角和÷180°）+2。此定理适用所有的平面多边形，包括凸多边形和平面凹多边形。

多边形的内角和公式可以根据多边形的边数n推导得出。该公式可以表示为：内角和 = (n - 2) × 180度 其中，n表示多边形的边数。该公式适用于任何多边形，包括三角形、四边形、五边形等等。

多边形内角和怎么求

1、多边形的内角和计算公式是N边形的内角和＝N*180°－360°＝N*180°－2*180°＝（N－2）*180°。由三条或三条以上的线段首尾顺次连接所组成的平面图形叫做多边形。按照不同的标准，多边形可以分为正多边形和非正多边形、凸多边形及凹多边形等。

2、多边形的内角和怎么求 ：内角和 = (n - 2) × 180度 其中，n代表多边形的边数。该公式适用于任何正多边形和凸多边形，但不适用于非凸多边形或自交多边形。具体步骤如下：确定多边形的边数，记为n。使用上述公式计算内角和，将n代入公式中。将计算出的内角和作为结果。

3、对于一个有n个边的多边形，其内角和可以用以下公式来计算：内角和=(n-2)×180度。这个公式基于多边形的特性，其中n代表多边形的边数。通过将n代入公式，我们可以计算出多边形的内角和。举例说明 对于一个三角形（三边形），它有3个边，那么根据内角和公式，它的内角和为：(3-2)×180度=180度。

4、多边形的内角和=（n-2）×180°。定义：一个多边形是由若干条线段组成的闭合图形，相邻的两条线段在端点处相交。每个内角和外角都是一个基本单元。性质：多边形的内角和受到边数的影响。随着边数的增加，内角和也相应增加。具体来说，多边形的内角和等于其边数与一个外角的和。

5、求多边形内角和的公式如下：已知内角和，边数=内角和÷180+2；已知一个内角，边数=360÷(180-内角)；已知一个外角，边数=360÷外角。已知多边形的内角和，求边数的公式：n边形的边=（内角和÷180°）+2。已知多边形的内外角的差，求边数的公式：边数=（内外角差＋360°）÷180°＋2。

6、正多边形内角和定理n边形的内角的和等于： （n － 2）×180°(n大于等于3且n为整数）。（1）任意凸形多边形的外角和都等于360°；（2）多边形对角线的计算公式：n边形的对角线条数等于1/2·n（n-3）；（3）在平面内，各边相等，各内角也都相等的多边形叫做正多边形。

一个多边形的内角和是多少°?

答案：180゜.解题过程如下：连结BC，∵∠E+∠D+∠EFD=∠1+∠2+∠BFC=180°，又∵∠EFD=∠BFC，∴∠E+∠D=∠1+∠2，∴∠A+∠B+∠C+∠D+∠E =∠A+∠ABD+∠ACE+∠1+∠2 =∠ABC+∠A+∠ACB =180゜．本题考点：三角形内角和定理。

一个多边形的内角和比四边形内角和多540度，则这个多边形的内角和为：360°+540°=900°。

一个多边形的内角和是900度，它是六边形。下面将对此问题进行详述：多边形 多边形，指由若干个线段组成的封闭图形，其中相邻两条线段的交点称为顶点，相邻的两个顶点所夹的角称为内角。不同的多边形拥有不同的内角和，其中三角形的内角和是180度，正方形的内角和是360度。

多边形内角和怎么求?

内角的和公式：（n－2）×180°(n大于等于3且n为整数），则多边形各内角度数为：（n － 2）×180°÷n。多边形内角和定理的推导及运用方程的思想来解决多边形内、外角的计算。在平面多边形中，边数相等的凸多边形和凹多边形内角和相等。但是空间多边形不适用。n边形内角和为（n-2)*180度。

多边形的内角和计算公式是N边形的内角和＝N*180°－360°＝N*180°－2*180°＝（N－2）*180°。由三条或三条以上的线段首尾顺次连接所组成的平面图形叫做多边形。按照不同的标准，多边形可以分为正多边形和非正多边形、凸多边形及凹多边形等。

多边形内角和等于：（n - 2）×180°(n大于等于3且n为整数）。多边形内角和定理证明：在n边形内任取一点O，连结O与各个顶点，把n边形分成n个三角形。因为这n个三角形的内角的和等于n180°，以O为公共顶点的n个角的和是360°。所以n边形的内角和是n180°-2×180°=(n-2)180°。

公式推导：对于一个有n条边的多边形，我们可以将其分成n-2个三角形，每个三角形的内角和为180度。因此，多边形的内角和为（n-2）×180度。这就是多边形内角和公式（n-2）×180的推导过程。应用范围：多边形内角和公式不仅可以用于计算多边形的内角和，还可以用于计算其他与角度有关的几何问题。

求多边形内角和的公式如下：已知内角和，边数=内角和÷180+2；已知一个内角，边数=360÷(180-内角)；已知一个外角，边数=360÷外角。已知多边形的内角和，求边数的公式：n边形的边=（内角和÷180°）+2。已知多边形的内外角的差，求边数的公式：边数=（内外角差＋360°）÷180°＋2。