频率分布直方图中位数怎么求（频率分布图怎么求中位数）

频率分布直方图中位数怎么算?

在样本中，有50%的个体小于或者等于中位数，同时也有50%的个体大于或者等于中位数。在中位数的左边和右边直方图的面积是相等的。从而我们可以根据这个来估算出中位数的大小值。频率分布直方图能清楚显示各组频数分布情况又易于显示各组之间频数的差别。它主要是为了将我们获取的数据直观、形象地表示出来。

中位数=x+0.5-(s1-s2-……-sn)/h 其中x表示中位数所在的那个方格的前边界数，例如这个方格表示在（15~18）那么x表示15，括号里面表示在这个方格前面的所有方格的面积，也就是频率，h表示中位数所在的方格的高。

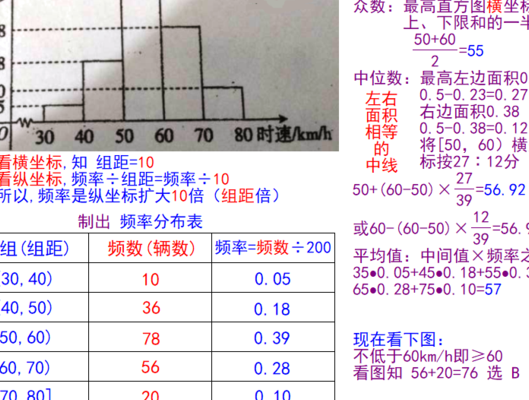
众数：频率分布直方图中最高矩形的底边中点的横坐标。算术平均数：频率分布直方图每组数值的中间值乘以频率后相加。加权平均数：加权平均数就是所有的频率乘以数值后的和相加。中位数：把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标。

怎样计算频率分布直方图的中位数?

平均数 = Σ(数据点值 × 频率) / 总频率 众数：众数是指频率最高的数值，即直方图中最高的柱子对应的数值。你可以简单地找到直方图中最高的柱子，并确定该柱子对应的数值即可。 中位数：中位数是将数据按升序排列后位于中间位置的数值。

中位数=x+0.5-(s1-s2-……-sn)/h 其中x表示中位数所在的那个方格的前边界数，例如这个方格表示在（15~18）那么x表示15，括号里面表示在这个方格前面的所有方格的面积，也就是频率，h表示中位数所在的方格的高。

从频率分布直方图可以估计出的几个数据：众数：频率分布直方图中最高矩形的底边中点的横坐标。算术平均数：频率分布直方图每组数值的中间值乘以频率后相加。加权平均数：加权平均数就是所有的频率乘以数值后的和相加。中位数：把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标。

频率分布直方图中的中位数，是衡量数据集中趋势的关键指标，它将样本分为两部分，一半的数据值小于或等于中位数，另一半则大于或等于。要计算中位数，首先需要理解每个矩形代表的数据频率，它们的总面积应等于0.5。

求频率分布图的中位数需要先计算出每个数据点的累计频率，并找到累计频率等于或最接近50%的数据点所对应的数值。频率分布图的定义 频率分布图是一种统计图形，用于展示数据的分布情况。它将数据分为不同的类别或区间，并绘制柱状图或直方图来表示每个类别或区间的频率。

在样本中，有50%的个体小于或者等于中位数，同时也有50%的个体大于或者等于中位数。在中位数的左边和右边直方图的面积是相等的。从而我们可以根据这个来估算出中位数的大小值。频率分布直方图能清楚显示各组频数分布情况又易于显示各组之间频数的差别。它主要是为了将我们获取的数据直观、形象地表示出来。

频率分布直方图的中位数怎么求

在样本中，有50%的个体小于或者等于中位数，同时也有50%的个体大于或者等于中位数，所以，在频率分布直方图中，在中位数的左边和右边直方图的面积是相等的。从而我们可以根据这个来估算出中位数的大小值。其实每个矩形的面积就是这组数据的频率。

中位数=x+0.5-(s1-s2-……-sn)/h 其中x表示中位数所在的那个方格的前边界数，例如这个方格表示在（15~18）那么x表示15，括号里面表示在这个方格前面的所有方格的面积，也就是频率，h表示中位数所在的方格的高。

中位数就是频率分布直方图面积的一半所对应的值，中位数=面积/2对应的横坐标，是找到左右面积都是0.5的横坐标。

中位数怎么求在频率直方图中

将频率直方图按照从小到大的顺序排列。将频率直方图中每个类别的频率值累加，得到累计频率值。例如频率直方图是[1，4，6，10]，则累计频率直方图是[1，5，11，21]。如果数据集的大小是奇数，则中位数恰好是数据集中位于频率直方图的中心的值，此处的中心为类间的中心点。

中位数=x+0.5-(s1-s2-……-sn)/h 其中x表示中位数所在的那个方格的前边界数，例如这个方格表示在（15~18）那么x表示15，括号里面表示在这个方格前面的所有方格的面积，也就是频率，h表示中位数所在的方格的高。

在样本中，有50%的个体小于或者等于中位数，同时也有50%的个体大于或者等于中位数，所以，在频率分布直方图中，在中位数的左边和右边直方图的面积是相等的。从而我们可以根据这个来估算出中位数的大小值。其实每个矩形的面积就是这组数据的频率。