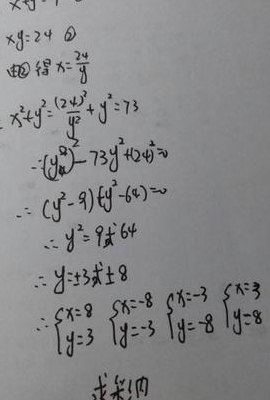高次方程（高次方程是几年级学的）

高次方程韦达定理

1、高次方程韦达定理x3+sx2+tx+u=0。韦达定理说明了一元二次方程中根和系数之间的关系。法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出了这条定理。 由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理。

2、韦达定理怎么运用 应用范围1：已知两个根其中的一个，就可以代入韦达定理的关系式里的任何来求得另一个根，并且还可以用另一个关系式来检验。应用范围2：根据根与系数的关系，把已知的两个根的和的相反数做所求方程的一次项系数，两根的积做常数项，而把二次项系数作为1，这样，就能作出这个方程。

3、韦达定理是关于一元二次方程根与系数之间关系的重要定理。无论一元二次方程\( ax^2 + bx + c = 0 \)是否有实数根，实系数的这类方程总能满足特定的规律。

4、方程根的性质：高次韦达定理描述了高次多项式方程的根的性质，对称多项式则是一种特殊的多元多项式，其各项关于变量具有对称性。这两者看似无关，但实际上有深刻的联系。

高次方程高次方程根与系数的关系

当我们面对形式为x^n + b(n-1)x^(n-1) + ... + b1x + b0 = 0的高次方程时，其根与系数之间存在着有趣的联系。首先，我们注意到一个基本的性质：所有根的和等于系数b(n-1)的负倒数，即 ∑x_i = -b(n-1)。

若高次方程有有理根，则有理根P/Q，P为常数项约数，Q为最高项约数。

高次方程韦达定理x3+sx2+tx+u=0。韦达定理说明了一元二次方程中根和系数之间的关系。法国数学家弗朗索瓦·韦达在著作《论方程的识别与订正》中建立了方程根与系数的关系，提出了这条定理。 由于韦达最早发现代数方程的根与系数之间有这种关系，人们把这个关系称为韦达定理。

根的和与系数的关系：x1 + x2 = -b/a。这一关系反映了一元二次方程的两个根的和等于负的系数b除以系数a的结果。 根的积与系数的关系：x1 * x2 = c/a。这一关系表示一元二次方程的两个根的积等于常数项c除以系数a的结果。

韦达定理是数学中的一个重要定理，它揭示了方程根与系数之间的关系。这个定理的表述非常简洁，但它的应用却是非常广泛的，不论是代数、几何还是物理学中都有广泛的应用。首先，我们来回顾一下韦达定理的基本内容。

关于方程根与系数的关系回答如下：关系 方程的根与系数之间的关系非常明显。首先，方程的根与系数之间的关系是线性的，也就是说如果我们改变方程中的系数，那么方程的根也会相应地改变。其次，方程的根与系数之间的关系是非常复杂的，因为方程的根不仅取决于系数的值，还取决于系数之间的相互作用。

高次方程的解题思路有什么?

高次方程是指含有两个或更多个未知数的多项式方程。解决高次方程的方法有很多，以下是一些常见的解题思路：因式分解法：将原方程化为几个一次因式的乘积，然后分别令每个因式等于零，得到一个或多个一元一次方程。解这些一元一次方程，就可以得到原方程的解。

公式法：有一些方程，已经研究出解的一般形式，成为固定的公式，可以直接利用公式。可解的多元高次的方程一般都有公式可循。函数图像法：利用方程的解为两个以上关联函数图像的交点的几何意义求解。

利用对称性来求解。对于一些具有对称性的高次方程，可以利用对称性来简化方程，从而更容易求解。利用递推关系来求解。对于一些具有递推关系的高次方程，可以利用递推关系来逐步求解。利用计算机软件来求解。对于一些复杂的高次方程，可以使用计算机软件来求解，例如MATLAB、Mathematica等。

如何解一元高次方程

1、一元高次方程的解法有多种方法，最常用的方法是配方法、因式分解法、求根公式法和牛顿迭代法等。配方法：将一元高次方程转化为一个多项式乘积等于零的形式，再分别解出每一个因式，即可得到方程的解。因式分解法：将一元高次方程进行因式分解，再分别解出每个因式，即可得到方程的解。

2、直接开平方法：（x+a）的平方=b。当b≥0时，x=-a±根号b；当b0时，方程没有实数根，这个方法可解全部一元多次方程。因式分解法：对于一些可以因式分解的多次方程式，可以将其转化为两个或多个一次方程式，然后解得未知数的值。

3、q2 = 4(p+2a)(r+a2)这是一个关于a的三次方程，利用上面一元三次方程的解法，我们可以 解出参数a。这样原方程两边都是完全平方式，开方后就是一个关于x 的一元二次方程，于是就可以解出原方程的根x。

4、他发现，高次方程根式解的问题最终归结于根的排列置换性质，而非特定次数的巧合解法。拉格朗日预解式因此应运而生，它标志着解一元高次方程策略的深化。拉格朗日预解式的核心是理解解方程的本质，即通过寻找对称多项式来打破根的对称性。

5、这个是三次方程一般来说在一般的练习中就是用观察法去解实际上如果你想了解一般三次方程的解法的话 我也可以简单给你介绍一下一元三次方程的标准型为aX^3+bX^2+cX+d=0，(a，b，c，d∈R，且a≠0)。