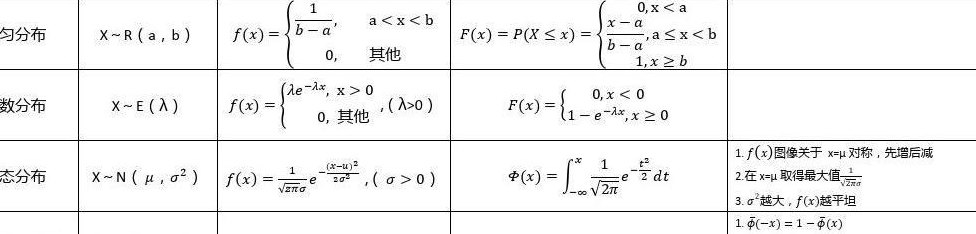分布函数和概率密度的关系（分布函数和概率密度的关系图）

分布函数和概率密度的关系

1、概率密度和分布函数的关系：分布函数是概率密度函数的积分，概率密度是分布函数的导数。概率密度 概率密度是指一个随机变量在某一取值附近的概率与该取值附近的区间长度的比值。概率密度是概率论和统计学中的一个重要概念，用于描述连续型随机变量的概率分布。

2、概率密度函数是分布函数的导数。分布函数是通过对概率密度函数求积分得到的。概率密度函数和分布函数是概率论中描述随机变量取值分布的两个基本工具。概率密度函数提供了随机变量取某个特定值附近的概率大小，而分布函数则提供了随机变量取值在某个区间内的概率。

3、分布函数和概率密度的关系是分布函数可以由概率密度函数求得，而概率密度函数也可以由分布函数求得。分布函数介绍：分布函数（英文Cumulative Distribution Function，简称CDF），是概率统计中重要的函数，正是通过它，可用数学分析的方法来研究随机变量。

概率密度和分布函数有何关系

1、概率密度和分布函数的关系：分布函数是概率密度函数的积分，概率密度是分布函数的导数。概率密度 概率密度是指一个随机变量在某一取值附近的概率与该取值附近的区间长度的比值。概率密度是概率论和统计学中的一个重要概念，用于描述连续型随机变量的概率分布。

2、分布函数是概率密度函数从负无穷到正无穷上的积分；在坐标轴上，概率密度函数的函数值y表示落在x点上的概率为y；分布函数的函数值y则表示x落在区间-∞上的概率。概率密度函数用于直观地描述连续性随机变量，表示瞬时幅值落在某指定范围内的概率，因此是幅值的函数。

3、在概率论中，概率密度函数与分布函数是密切相关的概念。概率密度函数，实质上是一个函数，其在所有实数上的积分结果代表一个具体的概率。它在坐标轴上的值反映了随机变量在特定点发生的可能性，可以被看作是连续随机变量瞬时概率的度量，它直接反映了变量的取值幅度。

概率密度与分布函数的关系是什么?

概率密度和分布函数的关系：分布函数是概率密度函数的积分，概率密度是分布函数的导数。概率密度 概率密度是指一个随机变量在某一取值附近的概率与该取值附近的区间长度的比值。概率密度是概率论和统计学中的一个重要概念，用于描述连续型随机变量的概率分布。

分布函数是概率密度函数从负无穷到正无穷上的积分；在坐标轴上，概率密度函数的函数值y表示落在x点上的概率为y；分布函数的函数值y则表示x落在区间-∞上的概率。概率密度函数用于直观地描述连续性随机变量，表示瞬时幅值落在某指定范围内的概率，因此是幅值的函数。

概率密度函数是分布函数的导数。分布函数是通过对概率密度函数求积分得到的。概率密度函数和分布函数是概率论中描述随机变量取值分布的两个基本工具。概率密度函数提供了随机变量取某个特定值附近的概率大小，而分布函数则提供了随机变量取值在某个区间内的概率。

菌落总数的计算？

1、菌落总数的计算公式是：CFU/g或CFU/mL = N × (1/d) × V。其中，N代表计数板上的菌落数量，d是取样体积（mL），V是稀释倍数。 计算方法包括以下步骤：a. 取一定量的样品，例如1g液体或1mL液体。b. 将样品按一定比例稀释，例如10^-4或10^-5倍。

2、菌落总数的计算公式为：菌落总数（CFU/g或CFU/mL）= N × (1/d) × V，其中，N为计数板上菌落数量；d为取样体积（mL）；V为稀释倍数。具体计算方法如下：取一定量的样品（比如，1g液体或1mL液体）。将样品按照一定比例进行稀释。如：稀释到10^-4或10^-5倍。得到不同浓度的稀释液。

3、菌落总数的计算主要依赖于以下公式：每克样品中的菌株数 = (平板上生长的平均菌落数 / 稀释液体积) * 稀释倍数 其中，C代表某一特定稀释度下平板上的平均菌落数（例如，200或300）。V是涂布平板时所使用的稀释液体积，通常以毫升（mL）为单位。M是稀释倍数，如1：10表示样品被稀释了10倍。

如何理解概率密度函数和分布函数之间的关系?

密度函数是一段区间的概率除以区间长度，值为正数，可大可小；而分布函数则是可以使用数学分析方法研究随机变量的一种曲线。密度函数一般只针对连续型变量，而分布函数则是既针对连续型也针对离散型随机变量。求解分布函数的时候要进行分类讨论和定积分计算，求解密度函数的时候需要进行求导。

结论：概率密度函数与分布函数是概率论与统计学中两个关键概念，它们各有特点，但又相互关联。下面是它们的区别和联系的详细解释：首先，概率密度函数和分布函数在概念上有所差异。

在概率论中，概率密度函数与分布函数是密切相关的概念。概率密度函数，实质上是一个函数，其在所有实数上的积分结果代表一个具体的概率。它在坐标轴上的值反映了随机变量在特定点发生的可能性，可以被看作是连续随机变量瞬时概率的度量，它直接反映了变量的取值幅度。

概率密度函数是分布函数的导数。分布函数是通过对概率密度函数求积分得到的。概率密度函数和分布函数是概率论中描述随机变量取值分布的两个基本工具。概率密度函数提供了随机变量取某个特定值附近的概率大小，而分布函数则提供了随机变量取值在某个区间内的概率。

分布函数是概率密度函数从负无穷到正无穷上的积分；在坐标轴上，概率密度函数的函数值y表示落在x点上的概率为y；分布函数的函数值y则表示x落在区间-∞上的概率。概率密度函数用于直观地描述连续性随机变量，表示瞬时幅值落在某指定范围内的概率，因此是幅值的函数。

概率密度函数和分布函数的关系

概率密度函数是分布函数的导数。分布函数是通过对概率密度函数求积分得到的。概率密度函数和分布函数是概率论中描述随机变量取值分布的两个基本工具。概率密度函数提供了随机变量取某个特定值附近的概率大小，而分布函数则提供了随机变量取值在某个区间内的概率。

概率密度和分布函数的关系：分布函数是概率密度函数的积分，概率密度是分布函数的导数。概率密度 概率密度是指一个随机变量在某一取值附近的概率与该取值附近的区间长度的比值。概率密度是概率论和统计学中的一个重要概念，用于描述连续型随机变量的概率分布。

分布函数和概率密度的关系是分布函数可以由概率密度函数求得，而概率密度函数也可以由分布函数求得。分布函数介绍：分布函数（英文Cumulative Distribution Function，简称CDF），是概率统计中重要的函数，正是通过它，可用数学分析的方法来研究随机变量。