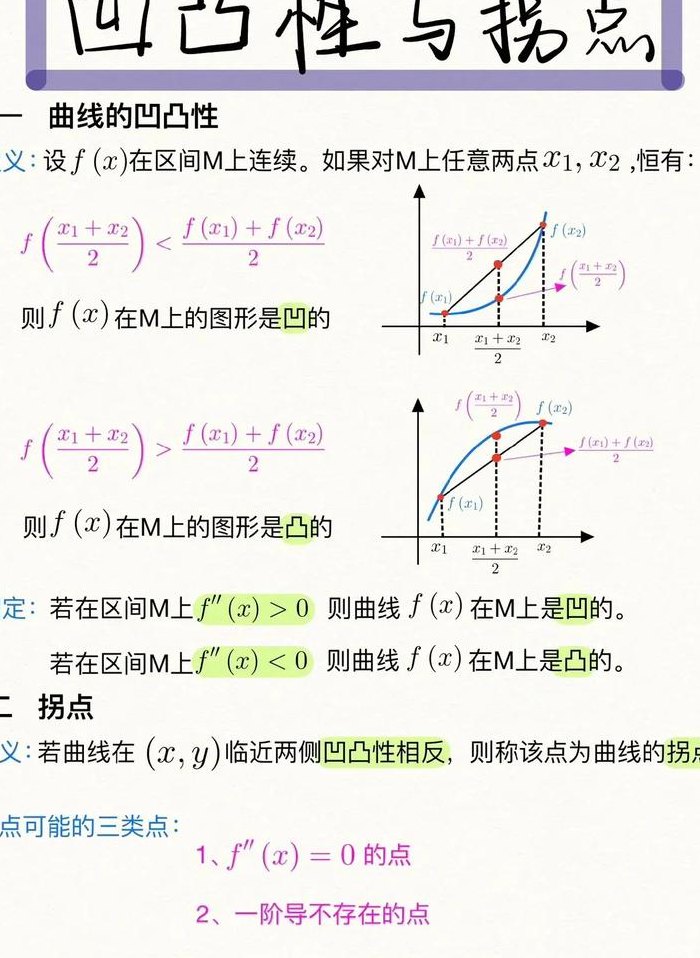
函数拐点的定义（二阶导数等于0是拐点吗）

什么是拐点?什么是零点和极值点?

1、零点，驻点，极值点指的都是函数y=f(x)的一个横坐标x0，而拐点指的是函数y=f(x)图像上的一个点。拐点：二阶导数为零，且三阶导不为零；驻点：一阶导数为零或不存在。极值点：若f(a)是函数f(x)的极大值或极小值，则a为函数f(x)的极值点，极大值点与极小值点统称为极值点。

2、拐点：又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。性质不同 在驻点处的单调性可能改变，在拐点处凹凸性可能改变。拐点：使函数凹凸性改变的点。驻点：一阶导数为零。

3、驻点和零点是x，极值点和拐点是坐标（x，y）。我们把导数f(x)的零点（即方程f(x)=0的根）叫做函数的驻点，也称临界点、稳定点，驻点可能是函数的极值点，在“这一点”，函数的输出值停止增加或减少，对于一维函数的图像，驻点的切线平行于x轴，对于二维函数的图像，驻点的切平面平行于xy平面。

什么是函数的拐点

1、函数的拐点指的是函数图像上的一个特定点，在该点处，函数的导数会发生从正到负或从负到正的改变。这一点标志着函数图形的变化趋势发生转变，可能是从上升变为下降，或者从下降变为上升。拐点的位置对于理解和分析函数的性质非常重要。

2、函数的拐点是指函数图形在该点发生凹凸性改变的点。拐点在函数图形上表现为图形从上升转变为下降，或者从下降转变为上升的地方。具体来说，如果一个函数在某点可导，且该点处的函数导数由正变负，那么这一点就是函数的拐点。拐点的数学定义与其在函数图形上的表现相吻合，它们是函数单调性改变的直接体现。

3、答案：函数的拐点是指函数图形在该点由上升转为下降或由下降转为上升的地方。更具体地说，拐点的数学定义是一个函数在这一点的前后的凹凸性发生改变。可以通过求解函数的导数并找到导数的拐点来找到原函数的拐点。解释： 拐点的定义：在函数的图像上，拐点是一个特殊的点，它改变了函数图形的走向。

函数的拐点是什么意思

1、拐点在数学上定义为函数的二阶导数发生符号变化的点。一阶导数是函数在某点的切线斜率，表示函数的变化率；二阶导数则反映了一阶导数的变化率，即函数斜率的增减速度。当二阶导数在一点处由正变负或由负变正时，就意味着函数在该点处由增函数变为减函数或由减函数变为增函数，这就是拐点。

2、拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。高等数学上指曲线上凸与下凹的分界点。

3、在数学领域，拐点指的是函数图形上某个点从上升变为下降或从下降变为上升的地方。简单来说，拐点就是函数曲线在某一点上开始改变其增减趋势的点。例如，在一条向上凸起的曲线中，拐点就是曲线开始或结束其向上弯曲的部分并转变为另一种弯曲方向的点。

4、函数的拐点是事物发展过程中运行趋势或运行速率的变化，也就是指凸曲线与凹曲线的连接点，当函数图像上的某点使函数的二阶导数为零，且三阶导数不为零时，这点即为函数的拐点。

什么是函数的拐点?怎样求拐点?

函数的拐点是指函数图形在该点由上升转为下降或由下降转为上升的地方。更具体地说，拐点的数学定义是一个函数在这一点的前后的凹凸性发生改变。可以通过求解函数的导数并找到导数的拐点来找到原函数的拐点。解释： 拐点的定义：在函数的图像上，拐点是一个特殊的点，它改变了函数图形的走向。

曲线拐点是指函数图像上某点附近的变化趋势发生改变的点。拓展知识：具体来说，对于一元函数，拐点是函数图像上曲线的凹凸性发生改变的点，即在该点附近函数图像的切线由凹向凸或由凸向凹变化。对于多元函数，拐点则是函数图像上曲面上的鞍点或鞍面上的最高点或最低点。

函数的拐点是函数图像从凸变凹或从凹变凸的关键点。

拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。

什么是拐点.

拐点是什么意思拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。高等数学上指曲线上凸与下凹的分界点。

拐点是指一个趋势或过程的转折点，即从增到减、从减到增，或者从一个方向转向另一个方向的点。拐点这一概念在多个领域都有涉及，具体解释如下： 数学领域中的拐点 在数学函数中，拐点是指函数图形上凹凸性发生变化的点。

拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点（即连续曲线的凹弧与凸弧的分界点）。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号（由正变负或由负变正）或不存在。对于二维函数的图像，驻点的切平面平行于xy平面。

拐点，又称反曲点，在数学上指改变曲线向上或向下方向的点，直观地说拐点是使切线穿越曲线的点(即曲线的凹凸分界点)。若该曲线图形的函数在拐点有二阶导数，则二阶导数在拐点处异号(由正变负或由负变正)或不存在。在生活中借指事物的发展趋势开始改变的地方(例如：经济运行出现回升拐点)。

函数的拐点是什么意思?

函数的拐点是指函数图形在该点发生凹凸性改变的点。拐点在函数图形上表现为图形从上升转变为下降，或者从下降转变为上升的地方。具体来说，如果一个函数在某点可导，且该点处的函数导数由正变负，那么这一点就是函数的拐点。拐点的数学定义与其在函数图形上的表现相吻合，它们是函数单调性改变的直接体现。

拐点是数学用语，也是生活用语。在数学领域，拐点指的是函数图形上某个点从上升变为下降或从下降变为上升的地方。简单来说，拐点就是函数曲线在某一点上开始改变其增减趋势的点。例如，在一条向上凸起的曲线中，拐点就是曲线开始或结束其向上弯曲的部分并转变为另一种弯曲方向的点。

函数的拐点指的是函数图像上的一个特定点，在该点处，函数的导数会发生从正到负或从负到正的改变。这一点标志着函数图形的变化趋势发生转变，可能是从上升变为下降，或者从下降变为上升。拐点的位置对于理解和分析函数的性质非常重要。