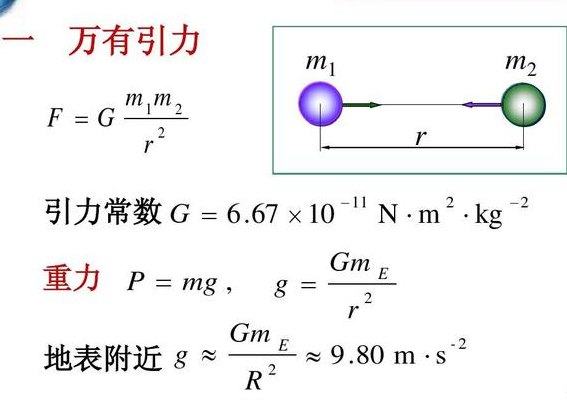
引力常量是多少(引力常数是多少)
同轴线介电常数
1、因为是材料和具体尺寸等限制的。当低耗的绝缘材料在实际中应用到柔性电缆上,电缆的尺寸规格必须保持不变,才能和现存的设备接口吻合。聚乙烯的介电常数为3,以空气(介电常数为1)为绝缘层的导线的阻抗为77 欧姆,如果以聚乙烯来填充绝缘空间的话,阻抗将减少为 51 欧姆。精确的标准是50欧姆。
2、同轴特性阻抗计算公式:Z0 = (120π/sqr(εr)) * η,其中,η为平面电磁波的波阻抗,εr为同轴内介质的相对介电常数,b为同轴线外导体内半径,a为内导体外半径。
3、先设导体球壳的电量为Q,根据高斯定律,在距球心距离为R的地方电场强度为Q/4pair2k(k为真空介电常数)。然后在a到b上对电场强度求积分来求电压U,可以根据高斯定理先求出电场强度E,然后再在径向对电场积分,就可以得到内外导体的电压,U=(q/(2*pi*ε)*ln(b/a)。
4、同轴电缆的核心结构是由一个不对称的同轴对组成,即内导体和外导体,两者通过绝缘介质保持轴向对齐。这种电缆广泛应用于多路载波通信、电视节目传输,以及高数据速率的数据信息传输,如UL2919屏幕线。 电缆的基本电气参数随频率和结构尺寸变化。有效电阻:随着频率上升而增加,与内外导体直径的比例关系不大。
5、介电常数是一个重要的岩石物理参数,人们尝试过很多方法来测量它,目前常用测量方法可根据频率不同分为:10kHz~200MHz频段,采用电容法;1~1100MHz,采用同轴线测量法;100MHz~2GHz频段则采用反射法、传输法和谐振腔法等。
引力常量
引力常量为G=67x10-11 N·m2 /kg2 引力常量的测定 牛顿发现了万有引力定律,但引力常量G这个数值是多少,连他本人也不知道。按说只要测出两个物体的质量,测出两个物体间的距离,再测出物体间的引力,代入万有引力定律,就可以测出这个常量。
引力常量,是物理学术语,公认的结果是卡文迪许测定的G值为754×10-11N·m2/kg2,最新的推荐的标准为G=67408(31)×10-11N·m2/kg2。通常取G=67×10-11N·m2/kg2,如果使用厘米克秒制则G=67×10-8 dyn·cm2/g2,其量纲为 L3 ·M-1·T-2。
引力常量G=67×10^-11 N·m^2/kg^2。
引力常量是多少?...
1、引力常量G=67×10^-11 N·m^2/kg^2。
2、引力常量,是物理学术语,公认的结果是卡文迪许测定的G值为754×10-11N·m2/kg2,最新的推荐的标准为G=67408(31)×10-11N·m2/kg2。通常取G=67×10-11N·m2/kg2,如果使用厘米克秒制则G=67×10-8 dyn·cm2/g2,其量纲为 L3 ·M-1·T-2。
3、引力常量是674×10^-11 N·m/kg。引力常量是一个自然界的常数,它是万有引力定律中的一个参数。万有引力定律描述了物体之间的引力与它们的质量以及它们之间的距离之间的关系。引力常量是这一关系中的比例系数,用于确定物体间引力的大小。
4、牛顿发现了万有引力定律,但引力常量G这个数值是多少,连他本人也不知道。按说只要测出两个物体的质量,测出两个物体间的距离,再测出物体间的引力,代入万有引力定律,就可以测出这个常量。卡文迪许测定的G值为754乘以10减11,现在公认的G值为67乘以10减11。
5、引力常量 GG 是一个物理常数,它的数值约为 674 \times 10^{-11}\,\mathrm{m^3\cdot kg^{-1}\cdot s^{-2}}674×10 11 m 3 kg 1 s 2 。
万有引力常数是多少,在地面上有效么
x10-11 N·m2/kg2 .它既然叫常数那它就有常数的性质:常数就是数值不会发生改变的数,是恒定不变的 。因此只要万有引力能用的地方它就恒定不变。我们的卫星,用的就是万有引力,地球绕太阳用的是万有引力,恒星间的运动也是万有引力,所以它不可能仅在地球表面上用。
万有引力常量是67×10^-11 m/kg·s。万有引力常量是物理学中非常重要的一个常数,用于描述物体之间的万有引力相互作用。它是由英国物理学家卡文迪许在1789年通过实验测量得到的。这个常量是自然界中的一个固定值,不会因为环境或者其他因素而改变。
万有引力常数是一个关键的物理常数,其值为67430e-11 米^3 / 千克秒^2。这一常数是万有引力定律的核心组成部分,用于描述物体间的引力相互作用。
引力常数是多少
1、引力常量,是物理学术语,公认的结果是卡文迪许测定的G值为754×10-11N·m2/kg2,最新的推荐的标准为G=67408(31)×10-11N·m2/kg2。通常取G=67×10-11N·m2/kg2,如果使用厘米克秒制则G=67×10-8 dyn·cm2/g2,其量纲为 L3 ·M-1·T-2。
2、引力常量G=67×10^-11 N·m^2/kg^2。
3、万有引力常数又称重力常数,其值约等于67259×10-11 千克-1·米3·秒-2,它是由英国物理学家亨利·卡文迪许在1798年通过扭秤实验测得的。
4、牛顿发现了万有引力定律,但引力常量G这个数值是多少,连他本人也不知道。按说只要测出两个物体的质量,测出两个物体间的距离,再测出物体间的引力,代入万有引力定律,就可以测出这个常量。卡文迪许测定的G值为754乘以10减11,现在公认的G值为67乘以10减11。
5、引力常量是674×10^-11 N·m/kg。引力常量是一个自然界的常数,它是万有引力定律中的一个参数。万有引力定律描述了物体之间的引力与它们的质量以及它们之间的距离之间的关系。引力常量是这一关系中的比例系数,用于确定物体间引力的大小。
6、牛顿重力常数 = 67300 × 10-11 m3 kg-1 s-2 自然界中任何两个物体都是相互吸引的,引力的大小与两物体的质量的乘积成正比,与两物体间距离的平方成反比。
引力常量G的值是多少?
引力常量 GG 是一个物理常数,它的数值约为 674 \times 10^{-11}\,\mathrm{m^3\cdot kg^{-1}\cdot s^{-2}}674×10 11 m 3 kg 1 s 2 。
引力常量,是物理学术语,公认的结果是卡文迪许测定的G值为754×10-11N·m2/kg2,最新的推荐的标准为G=67408(31)×10-11N·m2/kg2。通常取G=67×10-11N·m2/kg2,如果使用厘米克秒制则G=67×10-8 dyn·cm2/g2,其量纲为 L3 ·M-1·T-2。
引力常量G=67×10^-11 N·m^2/kg^2。
万有引力常量的数值为 G = 67 × 10^-11 N·m^2/kg^2,这一数值是由英国物理学家、化学家亨利·卡文迪许通过扭秤实验精确测得的。实验不仅验证了万有引力定律,也为库仑定律的验证提供了可能。在推导过程中,若将行星的轨道近似为圆形,根据开普勒第二定律,行星运动的角速度是恒定的。