三角形外心是什么（中心 重心 垂心 内心 外心）

三角形的外心,内心,中心,重心是什么

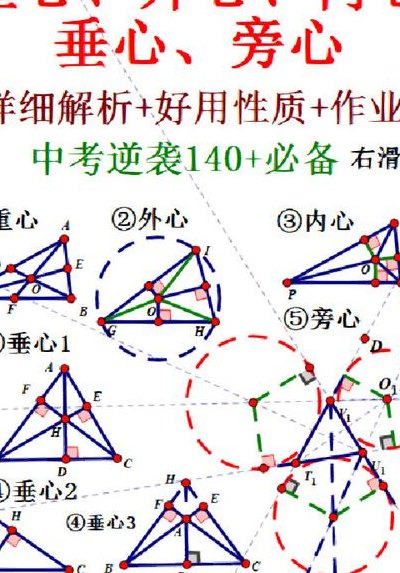
重心是三角形三条中线的交点 外心是三角形三条边的垂直平分线的交点 即外接圆的圆心 旁心，是三角形两条外角平分线和一条内角平分线的交点 正三角形中，中心和重心，垂心，内心，外心重合！垂心定理：三角形的三条高交于一点。该点叫做三角形的垂心 内心定理：三角形的三内角平分线交于一点。

外心：三角形外接圆的圆心，是三角形三边垂直平分线的交点.内心：三角形内接圆的圆心，是三角形的三个内角平分线的交点.中心：正多边形（如等边三角形）的外心、内心互相重复，也叫中心，是正多边形的旋转中心.重心：三角形三边中线的交点.垂心：三角形三条高的交点。

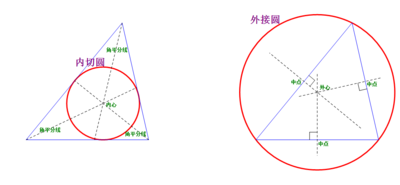
重心是三角形三条中线的交点，它将中线的每一条分成两部分，长度比为2：1。 内心是三角形三个角平分线的交点，或者是内切圆的圆心。它到三角形三边的距离相等。 外心是三角形三条中垂线的交点，或者是外接圆的圆心。它到三角形三个顶点的距离相等。 垂心是三角形三条高线的交点。

三角形的六心包括：重心，垂心，内心，外心，旁心，界心。 重心：三条中线的交点。 垂心：三天高线的交点。 内心：三条角平分线交点。 外心：三天垂直平分线的交点。 旁心：一内角的角平分线与另外两顶点处的外角平分线的交点。 界心：过三角形一顶点把三角形周长分为1：1的直线与三角形一边的交点。

外心：三角形外接圆的圆心，是三角形三边垂直平分线的交点。 内心：三角形内接圆的圆心，是三角形的三个内角平分线的交点。 中心：正多边形（如等边三角形）的外心、内心互相重复，也叫中心，是正多边形的旋转中心。 重心：三角形三边中线的交点。 垂心：三角形三条高的交点。

孔用弹性挡圈

1、孔用弹性挡圈是一种用于固定密封装置的标准零件，通常由弹簧钢制成。它通过在孔壁上产生一定的压力，实现对轴向力和载荷的传递和固定。弹性挡圈可有效地防止轴向滑移、减震和减少噪音。在各种机械设备和传动系统中广泛应用。

2、孔用弹性挡圈，轴用弹性挡圈—A型和B型的主要区别由以下几点；形状不同：A型采用板材冲切工艺制成，截面呈方形或者矩形。B型系采用线材冲切工艺制成，截面呈圆形。制作工艺不同：A型采用板材冲切工艺制成，B型系采用线材冲切工艺制成。

3、孔用弹性挡圈属于紧固件学科的一级分类，它在标准件领域中占据重要地位，作为三级学科的代表。它还有其他同义称呼，如孔用卡簧、孔用挡卡或孔用卡环。在更具体的分类中，它与轴用弹性挡圈，E形弹性挡圈，以及开口挡圈等概念相关联，这些都是一类用于不同应用场合的弹性支撑元件。

4、DIN472定义DIN472是工业紧固件领域中关于“孔用弹性挡圈”的德国标准，这个标准由德国工业标准协会（DIN）制定。孔用弹性挡圈，也被称为孔用卡环，用于限制零部件的轴向运动。

三角形的外心是什么?

1、定义：三角形的外心是三角形三条边的垂直平分线的交点，也是三角形外接圆的圆心。性质：三角形三条边的垂直平分线交于一点，该点即为三角形外接圆的圆心。三角形的内心 定义：三角形的内心是三角形三条内角平分线的交点，也是内切圆的圆心。

2、三角形的外心是三角形三边的垂直平分线的交点。详细解释如下：三角形的外心定义 三角形的外心是一个特殊的点，位于三角形外部，同时也是三角形三边垂直平分线的交点。换句话说，从三角形的每一个顶点出发，作其对应边的垂直平分线，这三条垂直平分线相交于一点，这一点就是三角形的外心。

3、三角形的外心是三条中垂线的交点，也就是外接圆的圆心。 三角形的内心是三条角平分线的交点，也就是内切圆的圆心。 三角形的垂心是三条高的交点。 三角形的重心是三条中线的交点。 在正三角形中，重心、垂心、内心和外心四个点会合于一点，这个点被称为正三角形的中心。

4、外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。

5、三角形内一点到三个顶点的距离相等，那么它是三角形的外心。外心指三角形三条边的垂直平分线（中垂线）的相交点。用这个点做圆心可以画三角形的外接圆。指三角形外接圆的圆心，一般叫三角形的外心。三角形的外心是三边中垂线的交点，且这点到三角形三顶点的距离相等。

三角形的外心是什么

1、三角形的外心 定义：三角形的外心是三角形三条边的垂直平分线的交点，也是三角形外接圆的圆心。性质：三角形三条边的垂直平分线交于一点，该点即为三角形外接圆的圆心。三角形的内心 定义：三角形的内心是三角形三条内角平分线的交点，也是内切圆的圆心。

2、三角形的外心是三角形三边的垂直平分线的交点。详细解释如下：三角形的外心定义 三角形的外心是一个特殊的点，位于三角形外部，同时也是三角形三边垂直平分线的交点。换句话说，从三角形的每一个顶点出发，作其对应边的垂直平分线，这三条垂直平分线相交于一点，这一点就是三角形的外心。

3、三角形外接圆的圆心叫做三角形的外心。三角形外接圆的圆心也就是三角形三边垂直平分线的交点，三角形的三个顶点就在这个外接圆上。

4、外心定理：三角形的三边的垂直平分线交于一点。该点叫做三角形的外心。

5、三角形的外心是三角形三条垂直平分线的交点。详细解释如下：三角形的外心概念 在几何学中，三角形的外心是一个特殊的点。它是三角形三条边的垂直平分线的交点。换句话说，从三角形每个顶点出发，向外部引一条垂线，这些垂线的中点所在的直线就是三角形的垂直平分线。

6、三角形内一点到三个顶点的距离相等，那么它是三角形的外心。外心指三角形三条边的垂直平分线（中垂线）的相交点。用这个点做圆心可以画三角形的外接圆。指三角形外接圆的圆心，一般叫三角形的外心。三角形的外心是三边中垂线的交点，且这点到三角形三顶点的距离相等。

三角形的外心一定是三角形内部吗?

不一定。三角形内一点到三个顶点的距离相等，那么它是三角形的外心。外心指三角形三条边的垂直平分线（中垂线）的相交点。用这个点做圆心可以画三角形的外接圆。指三角形外接圆的圆心，一般叫三角形的外心。三角形的外心是三边中垂线的交点，且这点到三角形三顶点的距离相等。

在三角形中，三个角的角平分线的交点是这个三角形内切圆的圆心而三角形内切圆的圆心就叫做三角形的内心，所以三角形的内心一定在这个三角形内；三角形外接圆的圆心叫做三角形的外心．因此，锐角三角形的外心在三角形内，直角三角形的外心在斜线上，钝角三角形的外心在三角形外。

不一定的，三角形的外心是三角形外接圆的圆心，用这个足够你来理解了，你可以画一个圆，再在圆里画一个内接三角形，你说可以画出一个三角形让圆心不在这个三角形内么？当然可以，这个时候这个三角形是钝角三角形，这个圆心就是三角形的外心，所以你的问题也就不是问题了。

外心是三角形的一个性质，指的是三角形三边的垂直平分线的交点。这个点在三角形内部，且到三角形的三个顶点的距离相等。外心也是三角形的一个重要特性，它具有一些有趣的性质和应用。首先，外心是三角形三边垂直平分线的交点，这意味着从外心到三角形的三个顶点的距离都是相等的。

不一定。重心、内心在三角形内部。重心是三角形三条中线的交点，内心是三角形三条角平分线的交点，中线和角平分线都在三角形的内部。外心是三角形三条边垂直平分线的交点，锐角三角形的外心在三角形的内部，直角三角形的外心在斜边的中点，而钝角三角形的外心在三角形的外部。

三角形的重心、垂心、内心和外心各是什么?

1、三角形的外心 定义：三角形的外心是三角形三条边的垂直平分线的交点，也是三角形外接圆的圆心。性质：三角形三条边的垂直平分线交于一点，该点即为三角形外接圆的圆心。三角形的内心 定义：三角形的内心是三角形三条内角平分线的交点，也是内切圆的圆心。

2、三角形的六心包括：重心，垂心，内心，外心，旁心，界心。 重心：三条中线的交点。 垂心：三天高线的交点。 内心：三条角平分线交点。 外心：三天垂直平分线的交点。 旁心：一内角的角平分线与另外两顶点处的外角平分线的交点。 界心：过三角形一顶点把三角形周长分为1：1的直线与三角形一边的交点。

3、重心是三条中线的交点，它到三角形三边的距离相等，且到三顶点的距离是它到对边中点的距离的两倍。内心是角平分线的交点，也是三角形内切圆的圆心，它到三角形三边的距离相等。外心是三条边垂直平分线的交点，也是三角形外接圆的圆心，它到三角形三个顶点的距离相等。