指数分布的方差（正态分布的方差）

指数分布的方差是什么?

1、指数分布的方差：D（X）=Var（X）=1/λ。指数分布与分布指数族的分类不同，后者是包含指数分布作为其成员之一的大类概率分布，也包括正态分布，二项分布，伽马分布，泊松分布等等。

2、指数分布，可以用来表示独立随机事件发生的时间间隔。指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。

3、均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12。二项分布，期望是np，方差是npq。泊松分布，期望是p，方差是p。指数分布，期望是1/p，方差是1/(p的平方)。

4、指数分布E(λ)：均值1/λ，方差：1/λ^2。卡方分布χ^2(n)：均值n，方差2n。

5、指数分布的参数为λ，则指数分布的期望为1/λ；方差为（1/λ）^2。E(X)==∫x*f(x)dx==∫λx*e^(-λx)dx=-(xe^(-λx)+1/λ*e^(-λx))|(正无穷到0)=1/λ。

指数分布的数学期望

指数分布的数学期望如下：指数分布的期望：E（X）=1/λ。指数分布的方差：D（X）=Var（X）=1/λ。

离散型随机变量X取可列个值时，它的数学期望要求级数∑|xi|pi收敛，否则数学期望不存在；连续型随机变量若在无限区间上取值，其数学期望是一个广义积分，要求积分绝对收敛，否则数学期望不存在。

D（x）指方差，E（x）指期望。方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。

某种电子元件的寿命x（以年计）服从数学期望为2的指数分布，各元件的寿命相互独立。随机取100只元件，求这100只元件的寿命之和大于180的概率。

另有一些现象并不直接表现为数量，例如人口的男女性别、试验结果的阳性或阴性等，但可以规定男性为1，女性为0，则非数量标志也可以用数量来表示。

请教指数分布的期望,方差,标准差的计算?

均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12。二项分布，期望是np，方差是npq。泊松分布，期望是p，方差是p。指数分布，期望是1/p，方差是1/(p的平方)。

指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。

计算方法：在计算指数分布的期望时，我们需要确定分布的参数λ。这通常通过数据拟合或统计分析来完成。根据实际数据和理论模型之间的拟合程度，我们可以估计λ的值，进而计算期望E[X]。

直接根据期望与方差的计算公式就可以如图求出期望是1，方差是1/6。（x-Ex）f（x）从负无穷到正无穷积分 E(X)就是X的平均值 参数为2的泊松分布，根据公式可知Eξ=Dξ=2，所以D(2ξ)=4Dξ=8。

期望值计算公式：E(X)=(n*M)/N [其中x是样本数，n为样本容量，M为样本总数，N为总体中的个体总数]，求出均值，这就是超几何分布的数学期望值。

期望值：方差：指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔，在排队论中，一个顾客接受服务的时间长短（等待时间等）也可以用指数分布来近似。

指数分布的期望、方差是多少?

1、期望值：方差：指数分布可以用来表示独立随机事件发生的时间间隔，比如旅客进机场的时间间隔，在排队论中，一个顾客接受服务的时间长短（等待时间等）也可以用指数分布来近似。

2、均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12。二项分布，期望是np，方差是npq。泊松分布，期望是p，方差是p。指数分布，期望是1/p，方差是1/(p的平方)。

3、指数分布：概率密度f(x)=λe^(-λx)，(x0)。期望EX=1/λ，方差DX=1/λ^2。概念 在做实验时，常常是相对于试验结果本身而言，我们主要还是对结果的某些函数感兴趣。

4、泊松分布P(λ)：均值为λ，方差为λ。几何分布GE(p)：均值。连续型分布：均匀分布U(a，b)：均值为(a+b)/2，方差为(a-b)^2/12。正态分布N(μ，σ)：均值：μ，方差：σ。

5、x~兀（入）指的是参数为λ的泊松分部。参数λ指的是分布的期望和方差都是λ。指数分布的参数为λ，则指数分布的期望为1/λ，方差为(1/λ)的平方。

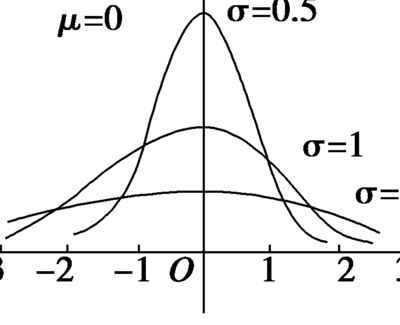
6、正态分布：若随机变量X服从一个数学期望为μ、方差为σ2的正态分布，记为N（μ，σ2）。当μ=0，σ=1时的正态分布是标准正态分布。其中期望是u，方差是σ的平方。

指数分布样本方差的期望E(S)怎么求

均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12。二项分布，期望是np，方差是npq。泊松分布，期望是p，方差是p。指数分布，期望是1/p，方差是1/(p的平方)。

指数分布的期望如下：定义：指数分布的期望定义为所有可能取值的加权和，其中权重的计算基于每个可能取值的概率。具体来说，如果一个随机变量X服从指数分布，其参数为λ（λ0），则X的期望E[X]为：E[X]=1/λ。

样本方差的期望等于总体方差，证明如下：设总体为X，抽取n个i。i。d。的样本X1，X2，...，Xn，其样本均值为Y = (X1+X2+...+Xn)/n。

六个常见分布的期望和方差是多少?

1、六个常见分布的期望和方差：均匀分布，期望是（a+b）/2，方差是（b-a）的平方/12。二项分布，期望是np，方差是npq。泊松分布，期望是p，方差是p。指数分布，期望是1/p，方差是1/(p的平方)。

2、其中期望是E(X)=1/λ，方差是D(X)=1/λ。

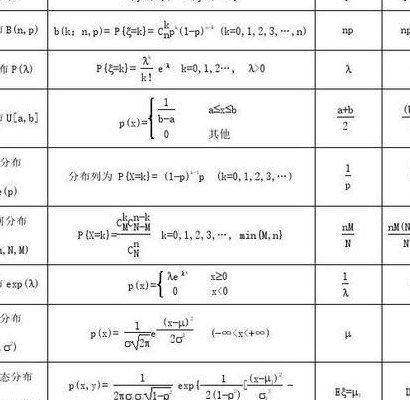
3、八大常见分布的期望和方差如下：0-1分布：E(X)=p，D(X)=p(1-p)。二项分布B(n，p)：P(X=k)=C(k\n)p^k·(1-p)^(n-k)，E(X)=np，D(X)=np(1-p)。

4、各种分布的期望与方差表如下：0-1分布B(1，p)：均值为p，方差为pq。二项分布B(n，p)：均值为np，方差为npq。泊松分布P(λ)：均值为λ，方差为λ。均匀分布U(a，b)：均值为(a+b)/2，方差为(a-b)^2/12。