全等三角形经典难题（全等三角形经典例题）

求两道全等三角形难题(附答案)

1、第一题：先证三角形ACD和AC’D’全等（Hl）∴角A=角A’∵角ACB=角A‘B’C‘=90°，AC=AC∴RT△ACB≌RT△A’C‘B（ASA）第二题：连接CE，DF。

2、． 如图13，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角 形，使所作的三角形与△ABC全等，这样的三角形最多可以画出___个。

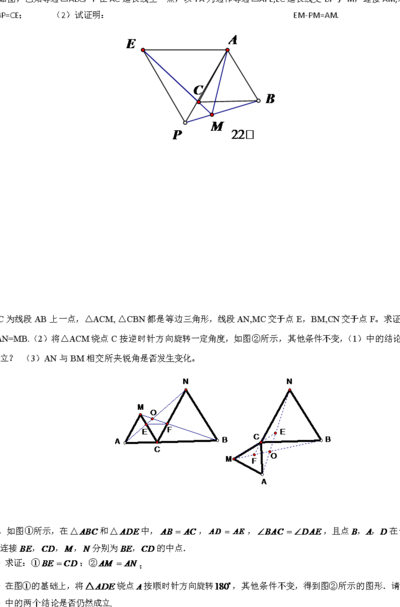
3、(2) AB与AC相等吗？若相等，请说明理由．21．如图，C是线段AE上一点，△ABC、△CDE都是等边三角形，AD与BC交于点M，BE与CD交于点N。试说明：(1)AD=BE；(2)MN//AE。

4、正常来说，验证两个全等三角形一般用边边边(SSS)、边角边(SAS)、角边角(ASA)、角角边(AAS)、和直角三角形的斜边，直角边(HL)来判定。下面是 为大家带来的八年级奥数全等三角形测试题及答案，欢迎大家阅读。

5、如图，△ABC和△DCE均是等边三角形，B、C、E三点共线，AE交CD于G，BD交AC于F。求证：CF=CG 如图，正△ABC中， D为AC边上的一个动点，延长AB至E，使BE=CD，连结DE，交BC于点P。求证：DP=PE 。

初二全等三角形难题,有多个小问的,越多越好(至少两个),要有图,谢谢...

第三个问用相似，GH平行AB，角EGH=角EAB，又角EAB=角BDC，所以三角形AGH与三角形FGH相似，得角GFH=角DGH=120度。

． 如图13，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角 形，使所作的三角形与△ABC全等，这样的三角形最多可以画出___个。

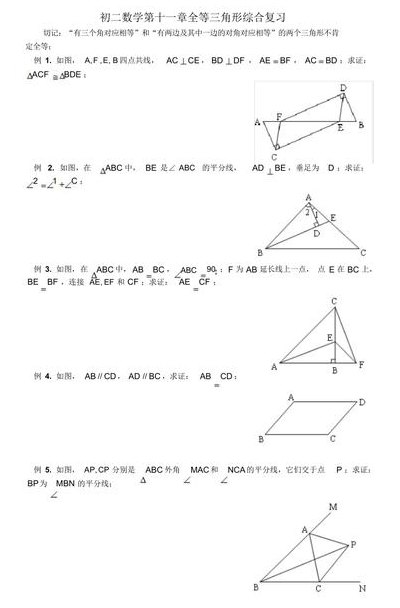
求证：有两边和第三边上的中线对应相等的两个三角形全等 ABC是等边三角形，点D，E，F分别是线段AB.BC.CA上的点，若DEF是等边三 角形 问 AD=BE=CF是否成立？并说明理由。

如图所示，已知ABCD和EDFG为正方形，连接AE和CG，M为AE的中点，求证DN⊥CG。因为时间关系，我只能先提供一个。

在四边形ABCD中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点做一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的关系，并加以证明。

求几道初二全等三角形的超难题,

． 如图13，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角 形，使所作的三角形与△ABC全等，这样的三角形最多可以画出___个。

求证：有两边和第三边上的中线对应相等的两个三角形全等 ABC是等边三角形，点D，E，F分别是线段AB.BC.CA上的点，若DEF是等边三 角形 问 AD=BE=CF是否成立？并说明理由。

如图，△ABC和△DCE均是等边三角形，B、C、E三点共线，AE交CD于G，BD交AC于F。求证：CF=CG 如图，正△ABC中， D为AC边上的一个动点，延长AB至E，使BE=CD，连结DE，交BC于点P。求证：DP=PE 。

奥数对青少年的脑力锻炼有着一定的作用，可以通过奥数对思维和逻辑进行锻炼，对学生起到的并不仅仅是数学方面的作用，通常比普通数学要深奥一些。

国际数学奥林匹克作为一项国际性赛事，由国际数学教育专家命题，出题范围超出了所有国家的义务教育水平，难度大大超过大学入学考试。下面是 无 为大家带来的初二年级奥数全等三角形试题及答案，欢迎大家阅读。

(4)若以A为锐角顶点，直角顶点D在x轴上的直角三角形ADF与以A、O、B为顶点的直角三角形全等，设F(a、b)，求a、b值(只需写出结果，不必写出解答过程)。

全等三角形的难题

1、一边上的中线，角评分线，高对应相等的三角形不一定全等，比如两个等腰三角形，底边上中线，角平分线，高三线合一，它们对应相等了，但两个等腰三角形不一定全等。

2、AD=AB， AC=AE， 角DAC = 60度+角BAC = 角BAE. 所以，三角形DAC和三角形BAE全等。所以，角ADF = 角ABF. 于是A，F，B，D四点共圆，于是角DFA=角DBA=60度。同理，角EFA=60度，所以FA是角DFE的平分线。

3、． 如图13，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角 形，使所作的三角形与△ABC全等，这样的三角形最多可以画出___个。

4、如图，△ABC和△DCE均是等边三角形，B、C、E三点共线，AE交CD于G，BD交AC于F。求证：CF=CG 如图，正△ABC中， D为AC边上的一个动点，延长AB至E，使BE=CD，连结DE，交BC于点P。求证：DP=PE 。

初二上册的数学难题(全等三角形),有没有

1、． 如图13，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角 形，使所作的三角形与△ABC全等，这样的三角形最多可以画出___个。

2、三角形ACD和三角形BCF是全等(两角一边分别相等)。所以AD和BF相等 在三角形ABC中，AB=AC，AD是高，求证：角BAD=角CAD。

3、求证：有两边和第三边上的中线对应相等的两个三角形全等 ABC是等边三角形，点D，E，F分别是线段AB.BC.CA上的点，若DEF是等边三 角形 问 AD=BE=CF是否成立？并说明理由。

4、八年级上册数学难题：《轴对称》和《全等三角形》。(人教) 求一些数学难题哦，一定要有难度。题越好，会追加悬赏的！我还要答案！最好给我文库哦。——咦，快给我解答啊！怎么没反应！？... 求一些数学难题哦，一定要有难度。

初二上册数学全等三角形难题

． 如图13，△ABC是不等边三角形，DE=BC，以D ，E为两个顶点作位置不同的三角 形，使所作的三角形与△ABC全等，这样的三角形最多可以画出___个。

第二题：设交点为O则可知AC=根号AO+OC=根号2*（AD+BC），这是由梯形等腰且对角线垂直解得，面积就是AC*BD/第三题：连AF求AEF全等于ABF，得BF=EF，在EFC中，EF=EC，根据等腰直角三角形定理。

在△ABC中，AB＝AC，∠A＝20°，D、E分别是AB、AC上的点，∠DCB＝50°，∠EBC＝60°，求∠DEB的度数。

求证：有两边和第三边上的中线对应相等的两个三角形全等 ABC是等边三角形，点D，E，F分别是线段AB.BC.CA上的点，若DEF是等边三 角形 问 AD=BE=CF是否成立？并说明理由。

如图，BD是∠ABC的平分线，DE⊥AB于E，∠C=90°，AB=36，BC=24，S△abc=150，求DC的长图：已知：如图，AD为△ABC中BC边上的中线，CE‖AB交AD的延长线于E。