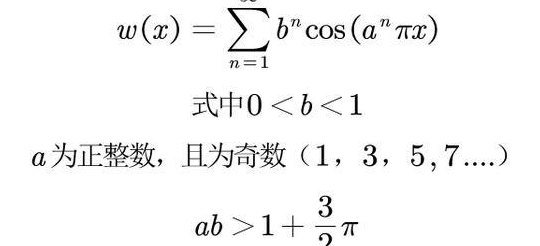魏尔斯特拉斯函数（魏尔斯特拉斯函数表达式）

魏尔斯特拉斯函数的构造

1、魏尔斯特拉斯的原作中给出的构造是：其中0a1，b为正的奇数，使得：这个函数以及它处处连续而又处处不可导的证明首次出现在魏尔斯特拉斯于1872年6月18日在普鲁士科学院出版的一篇论文中。证明这个函数处处连续并不困难。由于无穷级数的每一个函数项的绝对值都小于常数，而正项级数是收敛的。

2、连续性：简单来说，如果一个函数在某一点的极限值等于该点的函数值，那么我们就可以说该函数在该点连续。魏尔斯特拉斯函数在实数域上的每一点都满足这一条件，因此它是一个连续函数。可导性：可导性则是指函数在某一点的变化率存在。

3、魏尔斯特拉斯的原作中给出的构造是：，其中0 a 1，b 为正的奇数，使得：这个函数以及它处处连续而又处处不可导的证明首次出现在魏尔斯特拉斯于1872年6月18日在普鲁士科学院出版的一篇论文中。证明这个函数处处连续并不困难。

4、魏尔斯特拉斯定理是分析数学中的一个重要定理，它描述了任意连续函数可以用多项式逼近的性质。卡尔·特奥多尔·威廉·魏尔斯特拉斯（1815年10月31日-1897年2月19日），德国数学家，被誉为“现代分析之父”。生于威斯特法伦的欧斯腾费尔德，逝世于柏林。

5、由于无穷级数的每一个函数项matha^n \cos(b^n \pi x)/math的绝对值都小于常数matha^n/math，而正项级数 math \sum_{n=0} ^\infty a^n/math 是[[收敛]]的。由[[比较审敛法]]可以知道原级数一致收敛。

6、魏尔斯特拉斯逼近定理：闭区间上的连续函数可用多项式级数一致逼近。和闭区间上周期为2π的连续函数可用三角函数级数一致逼近。魏尔斯特拉斯常常同他的朋友——阿贝尔一起熬夜。当他成为世界上第一流的分析学家和欧洲最伟大的数学教师时，他对众多学生的第一个、也是最后一个忠告，就是“读阿贝尔”。

有高数大神帮忙看一下这是什么函数,全名哦,谢谢!

是一个分形函数，叫魏尔斯特拉斯函数，又叫weierstrass椭圆函数，处处连续但处处不可导。更多性质请百度。

∫∫Df(√(x^2+y^2))dxdy =∫∫Df(ρ)ρdρdθ=2π∫0，t f(ρ)ρdρ 所以这是一个变限函数，自变量为t。

好吧，这是个变上限定积分函数，你要知道x与被积对象t没有任何关系，故在积分是可以看成常数，积分过程中代入X作为所谓的上限，得到一个关于X的表达式，这时候这个表达式与t没有关系了，但是却与X有关系，这时候这个表达式就是x的函数，千万不要被积分蒙骗了。

魏尔斯特拉斯逼近定理

魏尔斯特拉斯逼近定理有两个：闭区间上的连续函数可用多项式级数一致逼近。闭区间上周期为2π的连续函数可用三角函数级数一致逼近。

魏尔斯特拉斯定理是分析数学中的一个重要定理，它描述了任意连续函数可以用多项式逼近的性质。卡尔·特奥多尔·威廉·魏尔斯特拉斯（1815年10月31日-1897年2月19日），德国数学家，被誉为“现代分析之父”。生于威斯特法伦的欧斯腾费尔德，逝世于柏林。

考虑P[a，b]（多项式空间）：利用魏尔斯特拉斯逼近定理，可知P[a，b]在C[a，b]稠密；并且P[a，b]是可数的。故C[a，b]为可分空间。

因为是闭区间，所以是有限区间 设为[a，b]那么只要构造一个周期为b-a的三角级数就可以了。

然而柯瓦列夫斯卡娅并不因此甘休，她找到了在柏林大学任教的著名数学家魏尔斯特拉斯，直接向他陈述自己的请求。这位年近花甲的教授迷惑了，他用怀疑的眼光看了看这个异邦的姑娘，然后向她提出了一个当时相当深奥的椭圆函数问题，这是教授前此一刻思考的。柯瓦列夫斯卡娅当场作了解

魏尔斯特拉斯函数处处为极值点吗?

1、导数不存在的点：在某些情况下，函数在某点可能不可导（例如尖点或间断点）。在这种情况下，我们可以直接比较该点的函数值与邻近点的函数值来确定极值。

2、在数学中，魏尔斯特拉斯函数(Weierstrass function)是一类处处连续而处处不可导的实值函数。魏尔斯特拉斯函数是一种无法用笔画出任何一部分的函数，因为每一点的导数都不存在，画的人无法知道每一点该朝哪个方向画。魏尔斯特拉斯函数的每一点的斜率也是不存在的。

3、极值点是函数在某个区间内取得最大值或最小值的点。在数学分析中，研究极值点的规律对于理解函数的性质和解决实际问题具有重要意义。极值点的规律主要包括以下几点：极值点的存在性：在一个有界闭区间上，连续函数必定存在极大值和极小值。这是由魏尔斯特拉斯定理保证的。

4、在数学中， 魏尔斯特拉斯函数是一类处处连续而处处不可导的实值函数。魏尔斯特拉斯函数是一种无法用笔画出任何一部分的函数，因为每一点的导数都不存在，画的人无法知道每一点该朝哪个方向画[1]。魏尔斯特拉斯函数的每一点的斜率也是不存在的。

5、不正确。f连续且在0处可导不能保证f在0的一个邻域内可导。（如果f可导，由达布定理可知导数一定连续，所以导数在0的一个邻域内是大于0的，即f单增。）反例可以由魏尔斯特拉斯函数构造。此函数是一个处处连续但处处不可导的函数，设为g。

证明魏尔斯特拉斯函数?简洁些

具体回答如下：不是所有的函数都可以求导；可导的函数一定连续，但连续的函数不一定可导（如y=|x|在y=0处不可导）。连续不可导的曲线 魏尔斯特拉斯函数是一种无法用笔画出任何一部分的函数，因为每一点的导数都不存在，画的人无法知道每一点该朝哪个方向画。

魏尔斯特拉斯的原作中给出的构造是：其中0a1，b为正的奇数，使得：这个函数以及它处处连续而又处处不可导的证明首次出现在魏尔斯特拉斯于1872年6月18日在普鲁士科学院出版的一篇论文中。证明这个函数处处连续并不困难。由于无穷级数的每一个函数项的绝对值都小于常数，而正项级数是收敛的。

在数学中， 魏尔斯特拉斯函数是一类处处连续而处处不可导的实值函数。魏尔斯特拉斯函数是一种无法用笔画出任何一部分的函数，因为每一点的导数都不存在，画的人无法知道每一点该朝哪个方向画[1]。魏尔斯特拉斯函数的每一点的斜率也是不存在的。

二元函数介值定理（又称为魏尔斯特拉斯中值定理）是数学分析中的一个重要定理。它说明了如果一个实数函数在一个闭区间上连续，那么它将取到这个区间内的任意两个值之间的所有值。证明二元函数介值定理的一种常见方法是通过反证法。