三集合容斥非标准公式（三集合容斥标准型和非标准型区别）

怎么能理解“三集合容斥”的公式?

A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。因为A、B、C与A交B两两的交集它们中都含A交B交C，然而ABC两两交集中我们应减两次，然而我们却将ABC两两交集中的A交B交C减了三次，所以我们应该加上多减的一次ABC的交集。

二集合容斥原理的公式为：|A∪B|=|A|+|B|-|A∩B|，三集合容斥原理的本质和二集合容斥原理是一样的，只不过由于又多了一个集合，公式和图形描述都变得更加复杂。其中A和B是两个集合，|A|表示集合A中的元素个数。

三个集合的容斥关系公式：AUBUC=A+B+C-A∩B-B∩C-C∩A+A∩B∩C。详细推理如下：等式右边改造＝｛-C∩A}+A∩B∩C。文氏图分块标记如右图图：1245构成A，2356构成B，4567构成C 等式右边（）里指的是下图的1+2+3+4+5+6六部分：那么AUBUC还缺部分7。

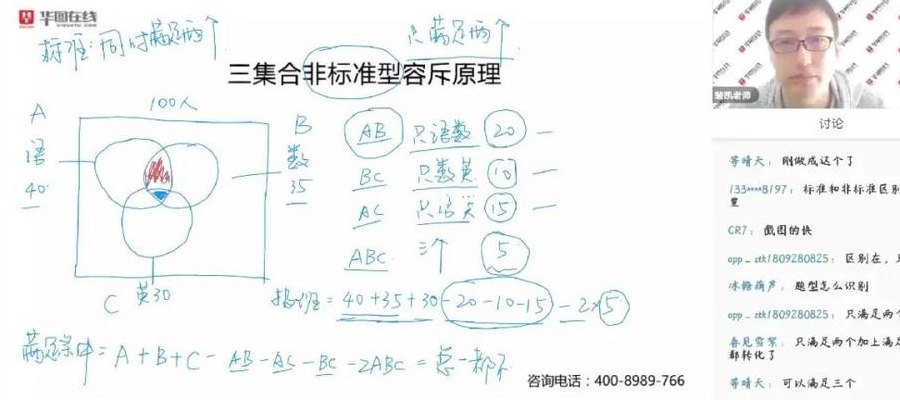
容斥问题三个集合的公式：A+B+C-A∩B-A∩C-B∩C+A∩B∩C=总数-三者都不满足的个数。把ABC想象成三个圆形纸片，ABC叠加在一起的面积等于ABC面积之和减去两两重叠的部分，但是中间三者重叠的部分减去了三次，相当于被挖空了，所以还得加上它。

三集合容斥原理标准型公式：Ⅰ+Ⅱ+Ⅲ-Ⅰ·Ⅱ-Ⅰ·Ⅲ-Ⅱ·Ⅲ+Ⅰ·Ⅱ·Ⅲ=总个数-三者都不满足个数。三集合容斥非标准型公式是A+B+C－（AB+BC+AC）+ABC＝总数－都不。

三者容斥问题3个公式是什么?

容斥问题3个公式如下：标准型： |A∪B∪C | = | A | + | B | + | C | - | A∩B | - | B∩C | - | C∩A | + | A∩B∩C |。非标准型：|A∪B∪C | = | A | + | B | + | C | -只满足两个条件的- 2×三个都满足的。

三者容斥问题 1）公式法：覆盖面积=A+B+C-两者交-2×三者交。2）解法二：若被计数的事物有A、B、C三类，那么，先把A、B、C三个集合的元素个数相加，然后减掉重复计算的部分。

粉笔三者容斥问题3个公式如下：标准型： |A∪B∪C | = | A | + | B | + | C | - | A∩B | - | B∩C | - | C∩A | + | A∩B∩C |。非标准型：|A∪B∪C | = | A | + | B | + | C | -只满足两个条件的- 2×三个都满足的。

三个集合容斥的公式是什么?

1、三集合容斥问题的核心公式如下：标准型： |A∪B∪C | = | A | + | B | + | C | - | A∩B | - | B∩C | - | C∩A | + | A∩B∩C |。非标准型：|A∪B∪C | = | A | + | B | + | C | -只满足两个条件的- 2×三个都满足的。

2、容斥问题3个公式如下：标准型： |A∪B∪C | = | A | + | B | + | C | - | A∩B | - | B∩C | - | C∩A | + | A∩B∩C |。非标准型：|A∪B∪C | = | A | + | B | + | C | -只满足两个条件的- 2×三个都满足的。

3、A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。因为A、B、C与A交B两两的交集它们中都含A交B交C，然而ABC两两交集中我们应减两次，然而我们却将ABC两两交集中的A交B交C减了三次，所以我们应该加上多减的一次ABC的交集。

4、A∪B∪C=A+B+C-A∩B-A∩C-B∩C+A∩B∩C。A∪B∪C=A+B+C-含有两种元素-2*含有三种元素。I=A∪B∪C+D=A+B+C-含有两种元素-2*含有三种元素+D。

5、三集合容斥问题的核心公式如下：标准型：|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|-|C∩A|+|A∩B∩C|。非标准型：|A∪B∪C|=|A|+|B|+|C|-只满足两个条件的-2×三个都满足的。列方程组：|A∪B∪C|=只满足一个条件的+只满足两个条件的+三个都满足的。

两个或三个集合的容斥公式是什么?

容斥原理（也称为容斥公式）是组合数学中的一个重要原理，用于计算多个集合的并、交和差的大小。对于两个集合A和B来说，容斥原理的表述如下：|A ∪ B| = |A| + |B| - |A ∩ B|其中，|A| 表示集合 A 的元素个数。

二集合容斥原理的公式为：|A∪B|=|A|+|B|-|A∩B|，三集合容斥原理的本质和二集合容斥原理是一样的，只不过由于又多了一个集合，公式和图形描述都变得更加复杂。详细推理如下： 等式右边改造 = {[（A+B - A∩B）+C - B∩C] - C∩A }+ A∩B∩C。

容斥原理三个公式有两个集合的容斥原理、三个集合的容斥原理、n个集合的容斥原理。两个集合的容斥原理。对于两个集合A和B，它们的交集记为A∩B，它们的并集记为A∪B，那么它们的容斥原理公式为：|A∪B|=|A|+|B|-|A∩B|。

容斥问题三个集合的公式：A+B+C-A∩B-A∩C-B∩C+A∩B∩C=总数-三者都不满足的个数。把ABC想象成三个圆形纸片，ABC叠加在一起的面积等于ABC面积之和减去两两重叠的部分，但是中间三者重叠的部分减去了三次，相当于被挖空了，所以还得加上它。