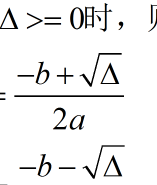二次函数的求根公式（二次函数的求根公式是什么）

二次函数求根公式法

二次函数求根公式是：x=[-b±√（b2-4ac）]/（2a）。二次函数（quadratic function）的基本表示形式为y=ax+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

二次函数求根公式是x=[-b±√(b2-4ac)]/(2a)。一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数。二次函数的求根公式 解ax^2+bx+c=0的解。

二次函数两个根的公式如下：要求解二次方程的两个根，我们可以使用一元二次方程的求根公式。一元二次方程的一般形式为 $ax^2 + bx + c = 0$；在这个公式中，$\pm$ 表示可以取两个不同的符号，从而得到方程的两个根。

二次函数求根公式如下：根据二次函数的一般形式f(x)=ax^2+bx+c=0，要求解该方程，可以使用以下根公式：x=(-b ±√(b^2-4ac))/2a这里±表示两个解，分别为加号和减号情况下的解。

二次函数与二次方程的根怎么求?

二次函数的求根公式：x = [-b±√(b2-4ac)]/(2a)。证明：解ax^2+bx+c = 0 的解。

二次函数两个根的公式如下：要求解二次方程的两个根，我们可以使用一元二次方程的求根公式。一元二次方程的一般形式为 $ax^2 + bx + c = 0$；在这个公式中，$\pm$ 表示可以取两个不同的符号，从而得到方程的两个根。

二次函数表达式为y=ax+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。如果令y值等于零，则可得一个二次方程。该方程的解称为方程的根或函数的零点。大约在公元前480年，古巴比伦人和中国人已经使用配方法求得了二次方程的正根，但是并没有提出通用的求解方法。

二次函数求根公式是什么?

1、二次函数的求根公式x=【-b±√（b^2-4ac）】/（2a）。二次函数的基本表示形式为y=ax+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。二次函数表达式为y=ax+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。

2、二次函数求根公式是x=[-b±√(b2-4ac)]/(2a)。一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数。二次函数的求根公式 解ax^2+bx+c=0的解。

3、二次函数的求根公式：x = [-b±√(b2-4ac)]/(2a)。证明：解ax^2+bx+c = 0 的解。

二次函数求根公式

1、二次函数求根公式是：x=[-b±√（b2-4ac）]/（2a）。二次函数（quadratic function）的基本表示形式为y=ax+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。

2、二次函数的求根公式：x = [-b±√(b2-4ac)]/(2a)。证明：解ax^2+bx+c = 0 的解。

3、二次函数求根公式是x=[-b±√(b2-4ac)]/(2a)。一般地，自变量x和因变量y之间存在如下关系：一般式：y=ax2+bx+c(a≠0，a、b、c为常数)，则称y为x的二次函数。二次函数的求根公式 解ax^2+bx+c=0的解。

4、二次函数求根公式如下：根据二次函数的一般形式f(x)=ax^2+bx+c=0，要求解该方程，可以使用以下根公式：x=(-b ±√(b^2-4ac))/2a这里±表示两个解，分别为加号和减号情况下的解。

请问二次函数的求根公式是什么?

二次函数的求根公式：x = [-b±√(b2-4ac)]/(2a)。证明：解ax^2+bx+c = 0 的解。

二次函数的求根公式x=【-b±√（b^2-4ac）】/（2a）。二次函数的基本表示形式为y=ax+bx+c（a≠0）。二次函数最高次必须为二次，二次函数的图像是一条对称轴与y轴平行或重合于y轴的抛物线。二次函数表达式为y=ax+bx+c（且a≠0），它的定义是一个二次多项式（或单项式）。

二次函数求根公式如下：根据二次函数的一般形式f(x)=ax^2+bx+c=0，要求解该方程，可以使用以下根公式：x=(-b ±√(b^2-4ac))/2a这里±表示两个解，分别为加号和减号情况下的解。

二次函数两个根的公式如下：要求解二次方程的两个根，我们可以使用一元二次方程的求根公式。一元二次方程的一般形式为 $ax^2 + bx + c = 0$；在这个公式中，$\pm$ 表示可以取两个不同的符号，从而得到方程的两个根。

二次函数公式法求根公式是x^2+bx+c=0，二次函数有很多种，ax^2+bx+c=0，(a不等于0，b^2-4ac0)的二次函数只是其中的一种，其解是x=[-b±(b^2-4ac)^(1/2)]/2a，若b^2-4ac 函数ax^2+bx+c+dy^2+ey+fxy+...=0，(未知数的最高项次不全为0)叫做多项式函数。

二次函数求根公式 二次函数有很多种，ax^2+bx+c=0，(a不等于0，b^2-4ac0)的二次函数只是其中的一种，其解是x=[-b±(b^2-4ac)^(1/2)]/2a，若b^2-4ac0，则函数将产生虚根，x=[-b±i(b^2-4ac)^(1/2)]/2a式中i为虚数。