几何分布(几何分布的期望)
几何分布怎样推导的?
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在第n次伯努利试验中,试验k次才得到第一次成功的机率。详细的说,是:前k-1次皆失败,第k次成功的概率。
几何分布期望公式推导:Dξ=∑(ξ-Eξ)^2*Pξ=∑(ξ^2+Eξ^2-2*ξ*Eξ)*Pξ=∑(ξ^2*Pξ+Eξ^2*Pξ-2*Pξ*ξ*Eξ)=∑ξ^2*Pξ+Eξ^2*∑Pξ-2*Eξ*∑Pξ*ξ。
几何分布是什么意思?
1、几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
2、几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在第n次伯努利试验中,试验k次才得到第一次成功的机率。详细的说,是:前k-1次皆失败,第k次成功的概率。
3、几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在第n次伯努利试验,才得到第一次成功的机率。详细的说,是:n次伯努利试验,前n-1次皆失败,第n次才成功的概率。
4、几何分布是一种离散型概率分布,用于描述在一系列伯努利试验中,试验r次才得到第一次成功的概率。具体来说,它表示在前r-1次都失败,在第r次成功的情况下的概率。在这种情景下,每次试验的成功概率为p,而失败概率则为q = 1-p。这意味着,随机变量X代表获得一次成功所需的试验次数。
5、几何分布是一种离散型概率分布,通常用于描述一系列独立试验中,直到某一次试验成功所需要的试验次数。在几何分布中,每次试验成功的概率是固定的,记为p。试验是相互独立的,这意味着每一次试验的结果不会影响到下一次试验的结果。
6、几何分布是离散型概率分布的一种。所描述的是n重伯努利试验成功的概率率。(所谓的伯努利实验指的是指在一次试验中只考虑两种结果:A发生和A不发生.在相同条件下将伯努利实验重复n次,每次实验A发生的概率都相同,称这样的一系列实验为n重伯努利实验。
几何分布的期望与方差是多少?
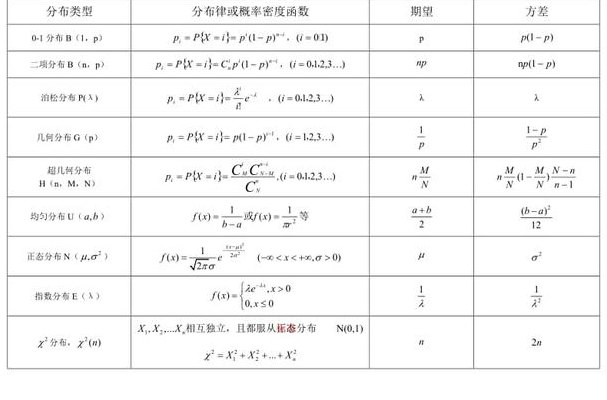
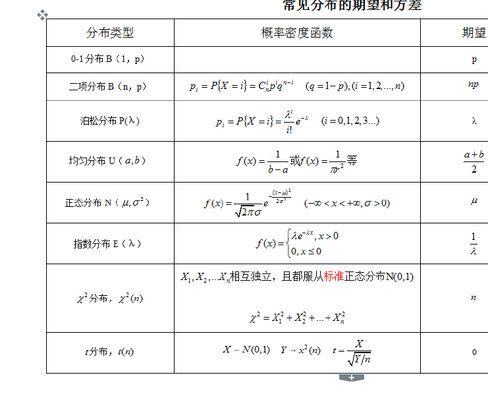
几何分布的期望是1/p,方差公式推导为s^2=[(x1-x)^2+(x2-x)^2+...(xn-x)^2]/(n),其中x为平均数。相关介绍:几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的几率。
几何分布,P(X=n)=(1p)^(n1)p,随着n增大呈等比级数变化,等比级数又称几何级数。这可能和以前几何学中无限分割图形得到的级数有关。
几何分布的期望和方差公式分别是E(n)=1/p、E(m)=(1-p)/p。几何分布是离散型概率分布,其中一种定义为前k-1次皆失败,第k次成功的概率。在伯努利试验中,成功的概率为p,若ξ表示出现首次成功时的试验次数,则ξ是离散型随机变量,它只取正整数,且有P(ξ=k)=(1-p)的(k-1)次方乘以p。
几何分布的期望EX=1/p,方差DX=(1-p)/p^2。超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出n个物件,成功抽出指定种类的物件的次数(不归还)。
几何分布的期望和方差是EX=nM/N,超几何分布是统计学上一种离散概率分布。它描述了从有限N个物件(其中包含M个指定种类的物件)中抽出n个物件,成功抽出该指定种类的物件的次数(不放回)。
几何分布为什么叫几何
几何数列、几何增长。几何数列:几何分布的分布列各项构成等比数列,而等比数列又被称为几何数列,因此得名。几何增长:几何分布是一种连续概率模型,其概率分布函数呈几何增长,这也是其得名的原因之一。
几何分布是离散型概率分布的一种。所描述的是n重伯努利试验成功的概率率。(所谓的伯努利实验指的是指在一次试验中只考虑两种结果:A发生和A不发生.在相同条件下将伯努利实验重复n次,每次实验A发生的概率都相同,称这样的一系列实验为n重伯努利实验。
那是因为他们都有几何上的对应和几何上的解释,或者说他们有时候就是源自几何上的例子得到这样的分布吧。
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
几何分布是一种离散型概率分布,通常用于描述一系列独立试验中,直到某一次试验成功所需要的试验次数。在几何分布中,每次试验成功的概率是固定的,记为p。试验是相互独立的,这意味着每一次试验的结果不会影响到下一次试验的结果。
几何分布的定义是什么?
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在第n次伯努利试验中,试验k次才得到第一次成功的机率。详细的说,是:前k-1次皆失败,第k次成功的概率。
几何分布(Geometric distribution)是离散型概率分布。其中一种定义为:在n次伯努利试验中,试验k次才得到第一次成功的机率。详细地说,是:前k-1次皆失败,第k次成功的概率。几何分布是帕斯卡分布当r=1时的特例。
几何分布是一种离散型概率分布,用于描述在一系列伯努利试验中,试验r次才得到第一次成功的概率。具体来说,它表示在前r-1次都失败,在第r次成功的情况下的概率。在这种情景下,每次试验的成功概率为p,而失败概率则为q = 1-p。这意味着,随机变量X代表获得一次成功所需的试验次数。