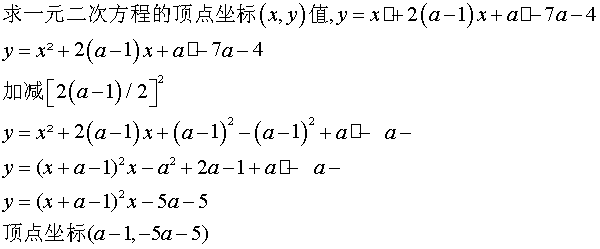一元二次方程顶点坐标（一元二次方程顶点坐标公式推导）

一元二次方程的顶点坐标公式是什么?

因此，研究抛物线y=ax+bx+c (a≠0)的图象，通过配方，将一般式化为y=a(x-h)+k 的形式，可确定其顶点坐标、对称轴抛物线的大体位置就很清楚了这给画图象提供了方便。

一元二次方程顶点坐标：［-b/2a，（4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。一元二次方程介绍 只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程。

一元二次方程顶点坐标：［-b/2a，（4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。

一元二次方程顶点坐标公式是：y=a(x-h)+k(a≠0，a、h、k为常数)，顶点坐标：(h，k)。

一元二次方程顶点坐标一般为[-b/2a，(4ac-b)/4a]。

一元二次方程顶点坐标：[-b/2a，(4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。一元二次方程的应用 增长率问题；行程问题；经济问题；工程问题。

一元二次方程顶点坐标怎么求?是有什么公式吗?

1、当a0，与b同号时（即ab0），对称轴在y轴左； 因为对称轴在左边则对称轴小于0，也就是- b/2a。当a0，与b异号时（即ab0），对称轴在y轴右。因为对称轴在右边则对称轴要大于0，也就是- b/2a0， 所以b/2a要小于0，所以a、b要异号。

2、一元二次方程顶点坐标公式是：y=a(x-h)+k(a≠0，a、h、k为常数)，顶点坐标：(h，k)。

3、一元二次方程顶点坐标：［-b/2a，（4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。

4、一元二次方程顶点坐标：［-b/2a，（4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。一元二次方程介绍 只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程。

一元二次方程式的顶点坐标

1、一元二次方程顶点坐标公式是：y=a(x-h)+k(a≠0，a、h、k为常数)，顶点坐标：(h，k)。

2、一元二次方程顶点坐标：[-b/2a，(4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。一元二次方程 只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程。

3、一元二次方程顶点坐标：[-b/2a，(4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。一元二次方程的应用 增长率问题；行程问题；经济问题；工程问题。

4、因此，研究抛物线y=ax+bx+c (a≠0)的图象，通过配方，将一般式化为y=a(x-h)+k 的形式，可确定其顶点坐标、对称轴抛物线的大体位置就很清楚了这给画图象提供了方便。

5、一元二次方程顶点坐标一般为[-b/2a，(4ac-b)/4a]。

一元二次函数顶点坐标公式

(1)、一般式： y = ax + bx + c (a，b，c为常数，a≠0)。

当a0，与b同号时（即ab0），对称轴在y轴左； 因为对称轴在左边则对称轴小于0，也就是- b/2a。当a0，与b异号时（即ab0），对称轴在y轴右。因为对称轴在右边则对称轴要大于0，也就是- b/2a0， 所以b/2a要小于0，所以a、b要异号。

一元二次函数顶点坐标公式是：y=ax+bx+c=a{x+b/（2a）}+（4ac-b）/（4a），顶点坐标：x=-b/（2a），y=（4ac-b）/（4a）。二次函数的基本表示形式为y=ax+bx+c（a≠0）。

一元二次方程顶点坐标：［-b/2a，（4ac-b)/4a]。顶点坐标是用来表示二次函数抛物线顶点的位置的参考指标，顶点式：y=a(x-h)+k(a≠0，k为常数）。

对称轴x=-b/2a，顶点坐标(-b/2a，(4ac-b^2)/4a)。一元二次函数的性质 (1)二次函数的图像是抛物线，抛物线是轴对称图形。对称轴为直线x=-b/2a。(2)二次项系数a决定抛物线的开口方向和大小。(3)一次项系数b和二次项系数a共同决定对称轴的位置。(4)常数项c决定抛物线与y轴交点。