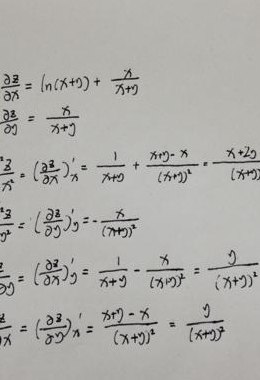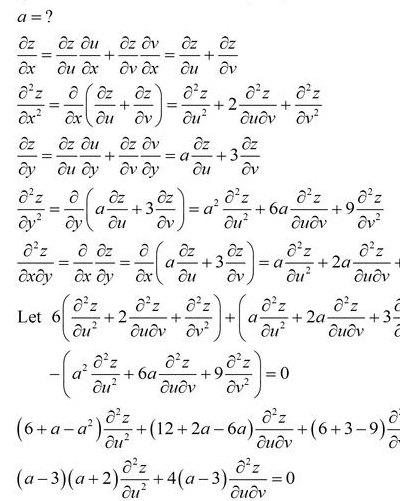偏导数怎么求（复合函数的二阶偏导数怎么求）

07-08 53阅读

偏导数怎么求?

1、综述：二元函数f(x，y)求偏导数，对x求偏导数时将y看作常量，求导；对y则将x看做常量。性质：连续函数，取极值（最大值或最小值）时偏导数为零。理解：一元函数，抛物线顶点处的导数都是0；推广到二元函数，则是对x，对y的偏导数都为0；多元一样。

2、偏导数基本公式：fx=(x^2)+2y *(x)=2x+2y。在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。偏导数在向量分析和微分几何中是很有用的。

（图片来源网络，侵删）

3、偏导数是只求对某一个变量的导数，与求普通导数完全一样，只要把另一个未知数看作常数即可。

4、对于单项式，对于x的偏导数仅保留x的指数，并将指数降低1。对于常数，偏导数为0。对于和式，可以逐项求偏导数。对于乘积，需要运用乘积法则来求解。链式法则对于复合函数f(g(x))，其中g(x)是一个函数，f(u)是另一个函数，求解复合函数的偏导数时可以利用链式法则。

5、怎么求偏导数？偏导数公式偏导数公式fx=(x^2)+2y *(x)=2x+2y。偏导数的表示符号为。计算多元函数的偏导数并不需要新的方法，若对某一个自变量求导，只需将其他自变量常数，用一元函数微分法即可。于是，一元函数的求导公式和求导法则都可以移植到多元函数的偏导数的计算上来。

6、求偏导的求法：求一元函数的偏导数的方法是一般按定义求。求多元函数的偏导数的方法是先对其中一个自变量求导，把其他自变量看成常数，再将一元函数的求导公式和求导法则移植到多元函数的偏导数的计算上来。偏导数反映的是函数沿坐标轴正方向的变化率。

（图片来源网络，侵删）

偏导数怎么求的

偏导数通过公式fx=(x^2)+2y*(x)=2x+2y计算。偏导数介绍：在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。偏导数在向量分析和微分几何中是很有用的。

求对 x 的偏导数，视 y 为常量，对 x 求导；求对 y 的偏导数，视 x 为常量，对 y 求导。

当函数z=f(x，y)在(x0，y0)的两个偏导数fx(x0，y0)与fy(x0，y0)都存在时，我们称f(x，y)在(x0，y0)处可导。如果函数f(x，y)在域D的每一点均可导，那么称函数f(x，y)在域D可导。

偏导数是只求对某一个变量的导数，与求普通导数完全一样，只要把另一个未知数看作常数即可。

先将$f(x，y)$在$x$处求导，得到$f(x，y)=2x+2y$ 将$y$视为常数，将$f(x，y)$带入偏导数的公式中，得到$\\frac{\\partial f}{\\partial x}=2x+2y$同理，可以求出关于$y$的偏导数$\\frac{\\partial f}{\\partial y}=2x+2y$。