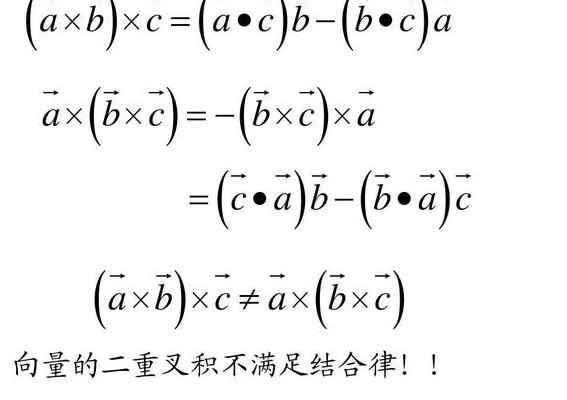叉乘运算法则（行列式叉乘运算法则）

叉乘(外积)的方向和运算法则

叉乘，也叫向量的外积、向量积。顾名思义，求下来的结果是一个向量，记这个向量为c。

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛，通常应用于物理学光学和计算机图形学中。

向量的叉乘运算法则为|向量c|=|向量a×向量b|=|a||b|sin，向量的外积不遵守乘法交换率，因为向量a×向量b=-向量b×向量a。向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。

向量叉乘的性质： 向量a × 向量b = 向量c，其中c的模长为|a||b|sin(θ)，θ为a与b的夹角，且c与a、b构成右手系中的右手螺旋方向。通过以上的解释，我们可以看到，尽管右手系和左手系在视觉呈现上有所差异，但在向量叉乘的世界里，它们都是数学语言中指引我们理解空间关系的强大工具。

向量外积（也称为叉乘）是向量运算中的一种，它的定义和计算公式如下：设两个向量A和B的坐标分别为（x1，y1，z1）和（x2，y2，z2），则它们的外积C可以表示为：C=A×B=（y1z2减y2z1，z1x2减z2x1，x1y2减x2y1）。

向量叉乘公式原理是向量c的方向与a，b所在的平面垂直，且方向要用“右手法则”判断，用右手的四指先表示向量a的方向，然后手指朝着手心的方向摆动到向量b的方向，大拇指所指的方向就是向量c的方向。向量积数学中又称：外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。

向量的叉乘运算符合什么法则?

叉乘不满足结合律。向量的数量积不满足结合律，即：（a·b)·c≠a·(b·c)；例如：（a·b)≠a·b。向量的数量积不满足消去律，即：由a·b=a·c(a≠0)，推不出b=c。|a·b|与｜a|·|b|不等价。

不满足，叉成后的方向符合右手螺旋法则。向量叉乘后的结果还是一个向量点乘是数，这个向量的方向用右手螺旋法则判断，叉乘后的新向量与原来两个都垂直，四指从一个向量转到另一个方向，拇指的方向就是新向量的方向。

向量的叉乘运算法则为|向量c|=|向量a×向量b|=|a||b|sin（a，b）。向量的外积不遵守乘法交换率，因为向量a×向量b=-向量b×向量a。

向量的叉乘运算法则为|向量c|=|向量a×向量b|=|a||b|sin，向量的外积不遵守乘法交换率，因为向量a×向量b=-向量b×向量a。向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。

sin(θ) 表示夹角 θ 的正弦值；n 是一个单位向量，其方向垂直于原来两个向量所在的平面，并符合右手法则。请注意，向量积的结果是一个向量，其大小等于两个向量的模长的乘积与它们之间夹角的正弦值的乘积，方向垂直于原来两个向量所在的平面，并满足右手法则。

两个向量的叉乘公式是什么?

1、拉格朗日公式 这是一个著名的公式，而且非常有用：a × (b × c) = b（a·c） c（a·b）向量叉乘的分配律的证明：ax(b+c)=axb + axc？这个可以用向量a，b，c的座标带进去，订边右边分别计算出结果，并证明相等 向量叉乘公式是什么，叉乘，也叫向量的外积、向量积。

2、向量b×向量a 在物理学中，已知力与力臂求力矩，就是向量的外积，即叉乘。

3、运算公式为：（1）|向量a|*|向量b|=—|向量b|*|向量a|；（2）|（向量a+向量b）|*|向量c|=|向量a|*|向量c|+|向量b|*|向量c|；（3）|向量a*向量b|=|向量c|=|a||b|sinθ。

4、二重向量叉乘化简公式及证明，可以简单地记成“BAC-CAB”。这个公式在物理上简化向量运算非常有效。需要注意的是，这个公式对微分算子不成立。这里给出一个和梯度相关的一个情形；这是一个霍奇拉普拉斯算子的霍奇分解的特殊情形。

数学中叉乘的公式是什么?

公式：a × b = |a| * |b| * sinθ 叉乘又叫向量的外积、向量积。点乘和叉乘的区别：点乘，也叫向量的内积、数量积。顾名思义，求下来的结果是一个数。向量a · 向量b=|a||b|cos。在物理学中，已知力与位移求功，实际上就是求向量F与向量s的内积，即要用点乘。

二维向量叉乘公式a（x1，y1），b（x2，y2），则a×b＝（x1y2－x2y1），不需要证明的就是定义的运算。三维叉乘是行列式运算，也是叉积的定义，把第三维看做0代入就行了。代数规则 反交换律：a×b=-b×a 加法的分配律：a×（b+c）＝a×b+a×c。

叉乘公式是a×（b×c）=b（ac）c（ab），向量积，数学中又称外积，叉积，物理中称矢积，叉乘，是一种在向量空间中向量的二元运算，它的运算结果是一个向量而不是一个标量。在数学中，向量（也称为欧几里得向量、几何向量、矢量），指具有大小（magnitude）和方向的量。

点乘，也叫数量积。结果是一个向量在另一个向量方向上投影的长度，是一个标量。叉乘，也叫向量积。结果是一个和已有两个向量都垂直的向量。

叉乘的计算公式为：a b = |a| |b| sin n，其中a和b是参与叉乘的两个向量，|a|和|b|分别是这两个向量的模，是这两个向量之间的夹角，n是与a和b都垂直的单位向量，叉乘的结果是一个向量。