什么是子集（什么是子集?）

子集是什么意思?

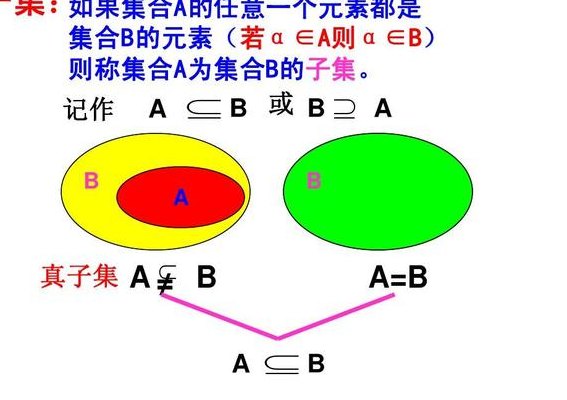
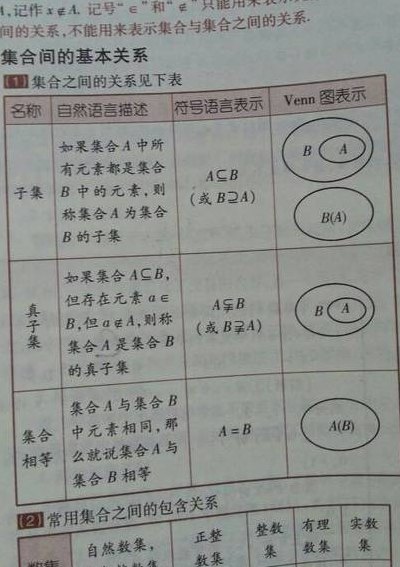
1、子集，为大集合中一部分的集合，故亦称部分集合。 [编辑本段]定义对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A，也说集合A是集合B的子集。

2、子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。集合论中，设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与集合B的交集（intersection），记作A∩B。

3、子集是一个数学概念，对于一个有n个元素的集合而言，其共有2^n个子集。其中空集和自身。另外，非空子集个数为 2^n -1 真子集个数为2^n -1；非空真子集个数为 2^n -2 定义：如果集合A的任意一个元素都是集合B的元素（任意a∈A则a∈B），那么集合A称为集合B的子集。

4、子集是数学中描述集合之间关系的一个重要概念。简单来说，子集是一个集合中的一部分元素，它们仍然作为一个整体构成一个新的集合。具体来说，如果集合A的每一个元素都是集合B的元素，那么集合A被称为集合B的子集。用符号表示即：若A属于B，则称A是B的子集。即AB。

什么是子集?

子集是数学中一个基本概念，指的是一个集合中的一部分元素组成的集合。具体来说，如果集合A的每一个元素都是集合B的元素，那么集合A就是集合B的子集。详细解释 子集概念在集合论中占据重要地位。简单来说，一个集合无论包含多少元素，它都可以有自己的子集。

子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。集合论中，设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与集合B的交集（intersection），记作A∩B。

子集，为大集合中一部分的集合，故亦称部分集合。 [编辑本段]定义对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A，也说集合A是集合B的子集。

子集是一个数学概念，对于一个有n个元素的集合而言，其共有2^n个子集。其中空集和自身。另外，非空子集个数为 2^n -1 真子集个数为2^n -1；非空真子集个数为 2^n -2 定义：如果集合A的任意一个元素都是集合B的元素（任意a∈A则a∈B），那么集合A称为集合B的子集。

子集是一个数学概念：对于两个非空集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说A含于B，或B包含A，称集合A是集合B的子集。根据子集的定义，我们知道任何一个集合是它本身的子集。

什么是子集。什么是真子集。举例说明。

1、A(读作B包含A)，称集合A是集合B的子集。真子集：如果A是B的子集，并且B中至少有一个元素不属于A，那么集合A叫做集合B的真子集。(2)注意两者的区别 子集比真子集范围大，子集里可以有全集本身，真子集里没有，还有，要注意非空真子集与真子集的区别，前者不包括空集，后者可以有。

2、(1)从定义上：集合A是集合B的子集，包括A是B的真子集和A与B相等两种情况，真子集是子集的特殊形式。(2)从性质上：空集是任何集合的子集，但不是任何集合的真子集，空集是任何非空集合的真子集。(3)从符号上：AB指AB或A=B都有可能。

3、真子集：如果集合A是B的子集，且A≠B，即B中至少有一个元素不属于A，那么A就是B的真子集，可记作：AB。所有亚洲国家组成的集合是地球上所有国家组成的集合的真子集；所有自然数的集合是所有整数的集合的真子集。

子集是什么意思

子集，为大集合中一部分的集合，故亦称部分集合。 [编辑本段]定义对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A，也说集合A是集合B的子集。

子集是一个数学概念，对于一个有n个元素的集合而言，其共有2^n个子集。其中空集和自身。另外，非空子集个数为 2^n -1 真子集个数为2^n -1；非空真子集个数为 2^n -2 定义：如果集合A的任意一个元素都是集合B的元素（任意a∈A则a∈B），那么集合A称为集合B的子集。

子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。符号语言：若a∈A，均有a∈B，则AB。

子集是一个数学概念，如果集合A的任意一个元素都是集合B的元素（任意a∈A则a∈B），那么集合A称为集合B的子集（subset）。对于两个非空集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说 A B(读作A包含于B)，或 B A(读作B包含A)，称集合A是集合B的子集。

子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。集合论中，设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与集合B的交集（intersection），记作A∩B。

子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。符号语言：若a∈A，均有a∈B，则AB。真子集：如果集合A是B的子集，且A≠B，即B中至少有一个元素不属于A，那么A就是B的真子集，可记作：AB。

什么叫子集

1、子集，为大集合中一部分的集合，故亦称部分集合。 [编辑本段]定义对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，我们就说集合A包含于集合B，或集合B包含集合A，也说集合A是集合B的子集。

2、子集 定义：设有集合A、B，若有x∈A，必有x∈B，那么称A是B的子集。记作AB，读作B包含A。定义：若两集合A、B满足AB且BA，称A与B相等，记作A=B。

3、子集是一个数学概念，对于一个有n个元素的集合而言，其共有2^n个子集。其中空集和自身。另外，非空子集个数为 2^n -1 真子集个数为2^n -1；非空真子集个数为 2^n -2 定义：如果集合A的任意一个元素都是集合B的元素（任意a∈A则a∈B），那么集合A称为集合B的子集。

4、子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。集合论中，设A，B是两个集合，由所有属于集合A且属于集合B的元素所组成的集合，叫做集合A与集合B的交集（intersection），记作A∩B。