海伦公式证明（海伦公式证明过程）

证明海伦公式的方法有哪些?

1、证明海伦公式的方法有以下几种： 几何法：首先，我们可以将三角形划分为两个直角三角形和一个矩形。然后，我们可以通过计算这两个直角三角形的面积和矩形的面积来得到三角形的面积。这种方法需要使用到勾股定理和矩形面积公式。 代数法：我们可以将海伦公式看作是一个关于a、b、c和s的二次方程。

2、首先，代数法是一种常用的证明方法。通过已知的三边长，可以构造一个关于三角形面积的二次方程，并利用求根公式求解该方程。这种方法需要一定的代数技巧，但能够直接得到海伦公式的表达式。其次，几何法也是证明海伦公式的一种常用方法。

3、s△abc = aha= ab×sinc = r p = 2r2sinasinbsinc = = 其中，s△abc = 就是著名的海伦公式，在希腊数学家海伦的著作《测地术》中有记载。海伦公式在解题中有十分重要的应用。

4、海伦公式又译作希伦公式、海龙公式、希罗公式、海伦－秦九韶公式，传说是古代的叙拉古国王希伦 （Heron，也称海龙）二世发现的公式，利用三角形的三条边长来求取三角形面积。

求海伦公式

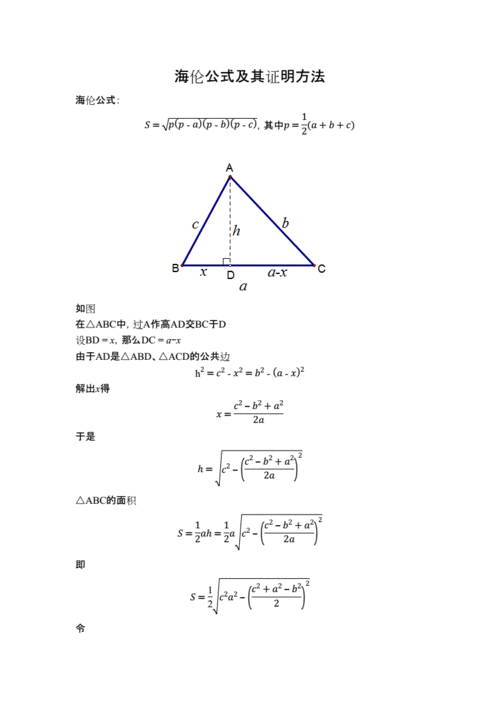
数学上的海伦公式：已知三角形三边a，b，c，则：（海伦公式）（p=(a+b+c)/2）：S=sqrt[p(p-a)(p-b)(p-c)]=sqrt[(1/16)(a+b+c)(a+b-c)(a+c-b)(b+c-a)]=1/4sqrt[(a+b+c)(a+b-c)(a+c-b)(b+c-a)]。

海伦公式：已知三角形三边长a，b，c。S=√P（P-a）（P-b）（P-c）。其中半周长P=（a+b+c）/2。海伦公式又译作希伦公式、海龙公式、希罗公式、海伦－秦九韶公式。它是利用三角形的三条边的边长直接求三角形面积的公式。

海伦公式是一种用于计算三角形面积的数学公式，表达式为：S = sqrt[p(p-a)(p-b)(p-c)]，其中p代表半周长，计算方式为p = (a + b + c) / 2，其中a、b、c分别是三角形的三条边长。该公式的核心思想是通过半周长和三角形边长的相互作用来求解面积。

怎样证明海伦公式的?

1、证明海伦公式的方法有以下几种： 几何法：首先，我们可以将三角形划分为两个直角三角形和一个矩形。然后，我们可以通过计算这两个直角三角形的面积和矩形的面积来得到三角形的面积。这种方法需要使用到勾股定理和矩形面积公式。 代数法：我们可以将海伦公式看作是一个关于a、b、c和s的二次方程。

2、证明海伦公式的方法有多种，其中包括但不限于代数法、几何法以及利用三角形的半周长与面积的关系进行证明。首先，代数法是一种常用的证明方法。通过已知的三边长，可以构造一个关于三角形面积的二次方程，并利用求根公式求解该方程。这种方法需要一定的代数技巧，但能够直接得到海伦公式的表达式。

3、解析如下：海伦公式：已知三角形三边长a，b，c。S=√P（P-a）（P-b）（P-c）。其中半周长P=（a+b+c）/2。海伦公式又译作希伦公式、海龙公式、希罗公式、海伦－秦九韶公式。它是利用三角形的三条边的边长直接求三角形面积的公式。

4、证明：如上图 根据勾股定理，得：此时化简得出海伦公式，证毕。