两直线垂直的公式(两直线垂直的公式斜率)
一般式两直线垂直关系公式
两直线垂直一般式公式为:A1A2+B1B2=0。直线一般式方程适用于所有的二维空间直线,它的基本形式是Ax+By+C=0(A,B不全为零)。
两直线垂直一般式公式:A1A2+B1B2=0。直线一般式方程适用于所有的二维空间直线。它的基本形式是Ax+By+C=0(A,B不全为零)。两直线的斜率乘积为-1,Ax+By+C=0,斜率为-A/B。
两直线垂直一般式公式:A1A2+B1B2=0。直线一般式方程适用于所有的二维空间直线。它的基本形式是Ax+By+C=0(A,B不全为零)。
关于一般式两直线垂直关系公式分享如下:两直线的斜率乘积为-1,Ax+By+C=0,斜率为-A/B。两直线垂直一般式公式A1A2+B1B2=0,直线一般式方程适用于所有的二维空间直线。它的基本形式是Ax+By+C=0(A,B不全为零)。
两直线垂直一般式公式计算:A1A2+B1B2=0。平行线一般式方程适合所有的二维空间平行线,其基本上方式是Ax+By+C=0(A,B不完整为零)。勾股定理是一个最基本的几何图形定律(Pythagorastheorem),它指的是直角三角形两条直角边的平均数相当于斜度的平方米。中国古人称直角三角形为勾股形。
如何用方程判断两直线平行与垂直
1、平行:直线的一般式方程是Ax+By+C=0,其中A和B是不为零的常数,C是任意常数。如果两条直线平行,那么它们的斜率相等,可以用以下公式表示:如果两条直线的一般式方程分别为Ax1+By1+C1=0和Ax2+By2+C2=0,如果它们平行,则有:A1/B1=-A2/B2。
2、可以通过斜率来判断两条直线是否互相平行或互相垂直,也可计算它们的交角。直线与某个坐标轴的交点在该坐标轴上的坐标,称为直线在该坐标轴上的截距。直线在平面上的位置,由它的斜率和一个截距完全确定。在空间,两个平面相交时,交线为一条直线。
3、在判断两直线的位置关系时,也可利用直线方程的一般式,由系数间的关系直接作出结论,设 , =0。(1) ‖ (2) 与 相交 ,则 。(3) 与 重合 (4) 。 两种距离 点P 到直线 的距离 ,两平行直线 和 之间的距离 。
4、直线方程如果平行的话,斜率相等;两条直线的斜率都是k,只是常数项不同。直线方程如果垂直的话,两条直线方程的斜率互为负倒数,即: k2=-1/k1。常数项要根据所过的点来确定。
5、平行与垂直的密码 当两条直线平行时,它们的斜率相等且截距不同,或是其中一条垂直于x轴,这是平行条件的密码。垂直条件则以斜率乘积为-1为特征,如同音乐中的和弦变化,构建出和谐的旋律。交角与距离的计算 直线ι与ι的交角和夹角,是几何中的关键度量。
两直线垂直的条件是什么
1、两直线垂直的条件是两条直线相交成直角,判断方法有2种。两条直线相交成直角时,这两条直线互相垂直,其中一条直线是另一条直线的垂线,这两条直线的交点叫垂足。设有两个向量a和b,a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0 。
2、条件是:两条直线在同一平面内。垂直,是指一条线与另一条线成直角,这两条直线互相垂直。通常用符号“⊥”表示。设有两个向量a和b,a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0。直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延长,长度无法度量。
3、两直线垂直的充要条件是:A1乘以A2加B1乘以B2等于0。不在同一平面内:两直线经过平移后相交成直角,则称两条直线互相垂直。线面垂直,则这条直线垂直于该平面内的所有直线,一条直线垂直于三角形的两边,那么它也垂直于另外一边。
4、垂直的定义是如果两条直线相交成直角,那么这两条直线互相垂直。
5、两条直线垂直的条件是斜率之积为-1。设两条直线的斜率分别为k1和k2。两条直线垂直,根据垂直线性的性质,斜率之积应该等于-1。这可以通过几何推导或者向量的方法进行证明。两条直线的斜率之积为-1,那么它们在坐标平面上的方向互相垂直。
6、两条直线垂直的条件是,它们的斜率互为负倒数。所以,与直线 Ax+By+C=0 垂直的直线方程可以表示为Bx-Ay+D=0 C和D可以相等,也可以不相等。
两条直线互相垂直公式
两条直线互相垂直公式:k1×k2=-1。两条线垂直公式:k1×k2=-1。垂直,是指一条线与另一条线成直角,这两条直线互相垂直。通常用符号“⊥”表示。设有两个向量a和b,a⊥b的充要条件是a·b=0,即(x1x2+y1y2)=0 。
两直线垂直一般式公式:A1A2+B1B2=0。直线一般式方程适用于所有的二维空间直线。它的基本形式是Ax+By+C=0(A,B不全为零)。两直线的斜率乘积为-1,Ax+By+C=0,斜率为-A/B。
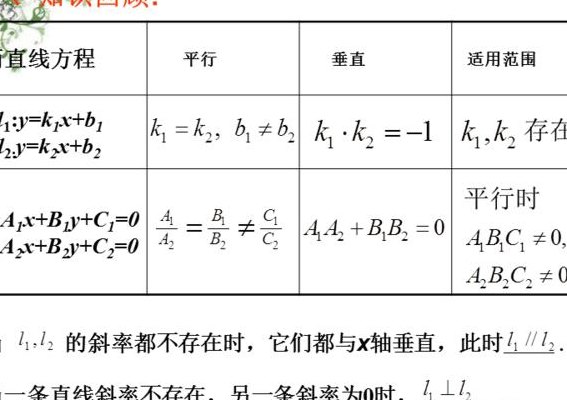
设有两条直线L1:y=k1x+b1 L2:y=k2x+b2 (1)L1和L2相交的充要条件:k1≠k2 (2)L1和L2平行的充要条件:k1=k2,b1≠b2 (3)L1和L2重合的充要条件:k1=k2,b1=b2 (4)L1和L2垂直的充要条件:k1*k2=-1 直线 直线由无数个点构成。直线是面的组成成分,并继而组成体。
垂直,是指一条线与另一条线相交并成直角,这两条直线互相垂直。设有两个向量a和b,a垂直b的充要条件是ab=0,即(x1x2+y1y2)=0 。对于立体几何中的垂直问题,主要涉及到线面垂直问题与面面垂直问题,而要解决相关的问题,其难点是线面垂直的定义及其对判定定理成立的条件的理解。
直线平行的判定与垂直的判定公式是什么?
直线平行的公式是Ax+By+C1=0和Ax+By+C2=0,直线垂直的公式是A1A2+B1B2=0。
平行公理和三角形中位线定理:两条直线平行,如果它们在同一个平面内,且没有其他直线与它们相交。这是一个非常重要的公理,它表明了在同一平面内的直线要么平行,要么相交。三角形的中位线平行于第三边,且等于第三边的一半。这个定理可以用来判断两条线段是否平行。
直线 直线由无数个点构成。直线是面的组成成分,并继而组成体。没有端点,向两端无限延伸,长度无法度量。直线是轴对称图形。它有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。在平面上过不重合的两点有且只有一条直线,即不重合两点确定一条直线。
平行线的判定定理:(1)两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。(内错角相等,两直线平行)(2)两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。(同旁内角互补,两直线平行)(3)两直线都与第三条直线平行,那么这两条直线也互相平行。
怎么判断两条直线平行垂直的公式
(1)平行:当两条直线l1和l2的斜率存在时,l1∥l2k1=k2;如果直线l1和l2的斜率都不存在,那么它们都与x轴垂直,则l1∥l2。
直线平行的公式是Ax+By+C1=0和Ax+By+C2=0,直线垂直的公式是A1A2+B1B2=0。
平行:直线的一般式方程是Ax+By+C=0,其中A和B是不为零的常数,C是任意常数。如果两条直线平行,那么它们的斜率相等,可以用以下公式表示:如果两条直线的一般式方程分别为Ax1+By1+C1=0和Ax2+By2+C2=0,如果它们平行,则有:A1/B1=-A2/B2。