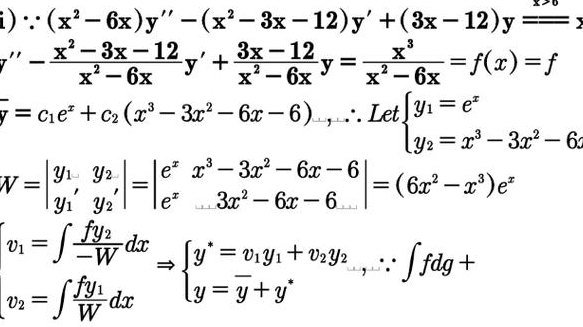二阶微分方程(二阶微分方程解法)
二阶微分方程的通解公式
1、二阶微分方程的通解公式:y+py+qy=f(x),其中p,q是实常数。自由项f(x)为定义在区间I上的连续函数,即y+py+qy=0时,称为二阶常系数齐次线性微分方程。若函数y1和y2之比为常数,称y1和y2是线性相关的。若函数y1和y2之比不为常数,称y1和y2是线性无关的。
2、二阶微分方程的3种通解公式如下:第一种:两个不相等的实根:y=C1e^(r1x)+C2e^(r2x)。第二种:两根相等的实根:y=(C1+C2x)e^(r1x)。第三种:一对共轭复根:r1=α+iβ,r2=α-iβ:y=e^(αx)*(C1cosβx+C2sinβx)。举例说明 求微分方程2y+y-y=0的通解。
3、第一种:由y2-y1=cos2x-sin2x是对应齐方程的解可推出cos2x、sin2x均为齐方程的解,故可得方程的通解是:y=C1cos2x+C2sin2x-xsin2x。第二种:通解是一个解集……包含了所有符合这个方程的解;n阶微分方程就带有n个常数,与是否线性无关。
4、第一种:y=C1cos2x+C2sin2x-xsin2x。由y2-y1=cos2x-sin2x是对应齐方程的解可推出cos2x、sin2x均为齐方程的解。第二种:通解是一个解集,包含了所有符合这个方程的解;n阶微分方程就带有n个常数,与是否线性无关。
5、二阶微分方程的3种通解公式是y=C1cos2x+C2sin2x-xsin2x,n阶微分方程就带有n个常数,Y=C1 e^(x/2)+C2 e^(-x)。第一种是由y2-y1=cos2x-sin2x是对应齐方程的解可推出cos2x、sin2x均为齐方程的解,故可得方程的通解是y=C1cos2x+C2sin2x-xsin2x。
二阶微分方程是什么?
在解释二阶微分方程之前,我们需要了解什么是微分方程。微分方程是一种描述未知函数及其导数之间关系的方程。而二阶微分方程则涉及到未知函数及其一阶、二阶导数。这种方程在物理学、工程学、经济学等领域有着广泛的应用。对于二阶线性微分方程,其解的形式通常与方程的系数p(x)、q(x)以及r(x)有关。
二阶微分方程的通解公式:y+py+qy=f(x),其中p,q是实常数。自由项f(x)为定义在区间I上的连续函数,即y+py+qy=0时,称为二阶常系数齐次线性微分方程。若函数y1和y2之比为常数,称y1和y2是线性相关的。若函数y1和y2之比不为常数,称y1和y2是线性无关的。
二阶微分方程是一种特殊的微分方程,其特点是方程中最高阶导数的阶数为二。换句话说,方程中二阶导数的次数是方程的阶数。例如,方程 (y)^4 + (y)^3 + xy^2 = 0 是一个二阶微分方程,因为其最高阶导数 y 的阶数是二。
微分方程的阶数是指方程中微分形式的最高阶数。所谓微分形式的阶,是指导数的形式是几次导数。如果方程含有y对x的二阶导数,即y,即y对x的导数再求导数,那就是二阶微分方程。
二阶微分方程如下:对于一元函数来说,如果在该方程中出现因变量的二阶导数,通常就称为二阶(常)微分方程,其一般形式为F(x,y,y,y)=0。在有些情况下,可以通过适当的变量代换,把二阶微分方程化成一阶微分方程来求解。
二阶常系数齐次微分方程怎么解?
1、二阶微分方程的3种通解公式是y=C1cos2x+C2sin2x-xsin2x,n阶微分方程就带有n个常数,Y=C1 e^(x/2)+C2 e^(-x)。第一种是由y2-y1=cos2x-sin2x是对应齐方程的解可推出cos2x、sin2x均为齐方程的解,故可得方程的通解是y=C1cos2x+C2sin2x-xsin2x。
2、二阶微分方程的通解公式:y+py+qy=f(x),其中p,q是实常数。自由项f(x)为定义在区间I上的连续函数,即y+py+qy=0时,称为二阶常系数齐次线性微分方程。若函数y1和y2之比为常数,称y1和y2是线性相关的。若函数y1和y2之比不为常数,称y1和y2是线性无关的。
3、二阶齐次微分方程的通解是:y=e^(αx)(C1cos(βx)+C2*sin(βx))。二阶常系数齐次线性微分方程一般形式为:y+py’+qy=0 ,其中p,q为常数。
4、Ay+By+Cy=e^mx 特解 y=C(x)e^mx Ay+By+Cy=a sinx + bcosx 特解 y=msinx+nsinx Ay+By+Cy= mx+n 特解 y=ax 二阶常系数线性微分方程是形如y+py+qy=f(x)的微分方程,其中p,q是实常数。
5、二阶常系数齐次线性微分方程的一般形式为:\( y + p(x) y + q(x) y = 0 \),其中 \( p(x) \) 和 \( q(x) \) 是关于 \( x \) 的函数,它们是常数时,方程成为常系数齐次线性微分方程。其特征方程为 \( r^2 + p(x)r + q(x) = 0 \)。
6、二阶非齐次线性微分方程的通解如下:y1,y2,y3是二阶微分方程的三个解,则:y2-y1,y3-y1为该方程的两个线性无关解,因此通解为:y=y1+C1(y2-y1)+C2(y3-y1)。方程通解为:y=1+C1(x-1)+C2(x^2-1)。