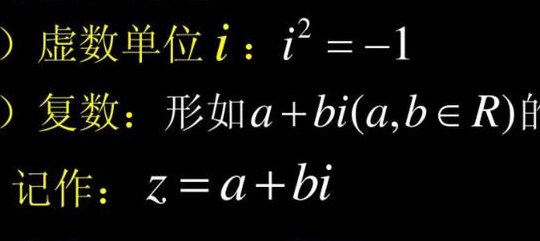复数的虚部（复数的虚部带正负号吗）

复数的虚部是什么?

1、C 试题分析：因为根据复数的除法运算得到 故可知复数的虚部为1，故选C.点评：对于复数的除法运算，既可以分母乘以其共轭复数，也可以将表达式整体变形，消项来求解得到。对于复数中虚部的理解要准确，是虚数单位前面的系数。

2、虚部是复数中的一部分。在详细解释虚部之前，我们先了解复数的概念。复数是一种数学表达形式，由实数和虚数两部分组成。其中，虚数部分即为虚部。虚数通常表示为“i”，它是复平面上的一个单位向量，并且与实轴垂直。而虚部的定义即为复数中对应虚数部分的值。

3、虚部是复数中与实数部分相对应的部分。在复数中，除了实部外，虚部是由虚数单位i构成的。虚数单位i是一个特殊的数，它的特性是i的平方等于-1。虚部通常与实部的运算方式类似，例如相加、相减、相乘和相除等，只是在与实部相乘时虚部会得到一个带有虚数单位的实系数。

4、C 试题分析：根据题意，由于复数 ，故可知实部为零，虚部为-2，故选C.点评：主要是考查了复数的乘除法运算以及复数的概念的运用，属于基础题。

5、y称为复数z的虚部。y=Imz。在笛卡尔直角坐标系中，y轴的值为虚部。利用实部和虚部可以判断两个复数是否相等，定义共轭复数，计算复数的模和辐角主值。复数分类：设复数为x+iy，则定义： 纯虚数：实数部分为零的复数被认为是纯虚数，即x=0。实数：虚数部分为零的复数是实数，即y=0。

虚部和实部是什么?

虚部和实部是复数的两个重要组成成分。在复数中，我们通常将一个复数表示为实部与虚部的和。这两部分共同构成了一个复数，其中实部是常规的实数部分，虚部则涉及到虚数单位i。接下来，我将详细解释虚部和实部的概念。实部 实部是复数的组成部分之一，代表的是复数在实数轴上的投影值。

实部是复数中的实数部分，虚部是复数中的虚数部分。在表达形式上，一个复数常常写成“实部 + 虚部”的形式。比如：复数 z 可以表示为 z = a + bi，其中 a 是实部，b 是虚部，i 是虚数单位。要注意的是虚数不一定比实数大或复杂。

实部与虚部是数学名词“复数”中的一个概念，把形如z=a+bi（a，b均为实版数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。

实部指的是一个复数的实数部分，即复数中实数的部分。实部表示复数在实数轴上的投影。虚部指的是一个复数的虚数部分，即复数中虚数的部分。虚部表示复数在虚数轴上的投影。一个复数可以表示为实部加上虚部的形式，例如，对于复数a+bi，a就是实部，b就是虚部。实部和虚部都是实数。

复数z的什么叫做虚部?

复数z的虚部，复数z=a+bi中的实数a称为复数z的实部，记作Rez=a，实数b称为复数z的虚部，记作 Imz=b。以复数作为自变量和因变量的函数就叫做复变函数，而与之相关的理论就是复变函数论。

对于复数z=x+iy，其中x，y是任意实数，y称为复数z的虚部。y=Imz。在笛卡尔直角坐标系中，y轴的值为虚部。利用实部和虚部可以判断两个复数是否相等，定义共轭复数，计算复数的模和辐角主值。复数分类：设复数为x+iy，则定义： 纯虚数：实数部分为零的复数被认为是纯虚数，即x=0。

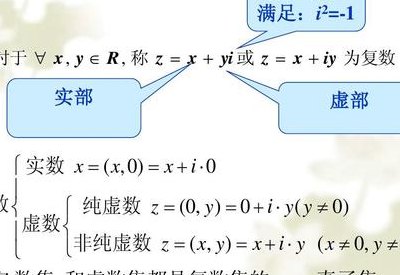
对于复数 z=x+iy，满足等式“i＝－1”，其中 x，y 是任意实数，x 称为复数 z 的实部，y 称为复数 z 的虚部。复数的概念来源于意大利数学家 Gerolamo Cardano，16 世纪，在他试图在找到立方方程的通解时，定义i为“虚构”。复数是普通实数的字段扩展，以便解决不能用实数单独解决的问题。

为什么复数有虚部和实部?它们有何意义?

1、复数的实部是指复数中实数部分的值，它与复平面上的平移有关。例如，对于信号x(t)=(cos(ωt)，sin(ωt))（其中ω为角频率），其瞬时值就是把变化率包含进来了，实部是信号本身的值，虚部是负变化率与角频率之比。

2、实部 实部是复数的组成部分之一，代表的是复数在实数轴上的投影值。简单来说，实部就是我们常规数学中所说的实数，可以用一个简单的数轴来表示。实部在复数中的表示没有虚数单位i的参与，是纯数值部分。在代数运算中，实部的运算法则与我们熟悉的实数运算法则相同。

3、实部和虚部是复数的两个组成部分，用来表示一个数在平面直角坐标系中的位置。实部表示该数在实数轴上的位置，而虚部表示它在虚数轴上的位置。例如，对于复数z=a+bi（a、b为实数），实部为a，虚部为b。实部和虚部在复数运算中都有重要的作用，它们可以通过加减乘除等运算来得到结果。

4、复数方程的解是由实部和虚部共同决定的。实部是指复数方程中不含虚部的那部分，而虚部则是指含有i的那部分。在复数范围内，虚部的变化不会改变复数的值，但是实部的取值会影响复数的模长。因此，对于复数方程的解，实部和虚部的取值都会影响其模长。

5、复数的实部在坐标系上是只存在在x轴上的点，虚部是只存在在y轴上的点。我们把形如 z=a+bi（a、b均为实数）的数称为复数。其中，a 称为实部，b 称为虚部，i 称为虚数单位。当 z 的虚部 b＝0 时，则 z 为实数；当 z 的虚部 b≠0 时，实部 a＝0 时，常称 z 为纯虚数。

复数实部和虚部是什么怎么表示

1、实部与虚部是数学名词“复数”中的一个概念，把形如z=a+bi（a，b均为实版数）的数称为复数，其中a称为实部，b称为虚部，i称为虚数单位。

2、复数可以分为实部和虚部，记为a+ib，在直角坐标系中，横轴代表实数，纵轴代表虚数，以A（a，b）代表实数A=a+ib；在极坐标系中，以原点作为始点，A（a，b）作为终点的矢量代表该虚数，用A（r，θ）表示，其中r=(a平方+b平方）的开二次方，θ = arctg（b/a)。

3、实部是指复数的实数部分，可以用符号Re(z)表示，对于复数z=a+bi，实部就是a。虚部是指复数的虚数部分，可以用符号Im(z)表示，对于复数z=a+bi，虚部就是b。延伸内容：我们可以通过复数的实部和虚部来进行复数的运算、表示和分析。

4、复数的实部和虚部是指复数的数学形式中的实部和虚部。复数通常用z表示，即z=a+bi，其中a被称为实部，b被称为虚部 。如果z的虚部等于零，则称z为实数；如果z的虚部不等于零，则当实部等于零时，常称z为纯虚数 。

5、代数表示方法 在英文中，实数是 Real Quantity，所以一般取 Real 的前两个字母 “Re” 表示一个复数的实部；虚数是 Imaginary Quantity，所以，一般取 Imaginary 的前两个字母 “Im” 表示一个复数的虚部。例如：Re(2+3i)=2， Im(2+3i)=3；Re(-38i)=0， Im(-38i)=-38。

6、复数的实部在坐标系上是只存在在x轴上的点，虚部是只存在在y轴上的点。我们把形如 z=a+bi（a、b均为实数）的数称为复数。其中，a 称为实部，b 称为虚部，i 称为虚数单位。当 z 的虚部 b＝0 时，则 z 为实数；当 z 的虚部 b≠0 时，实部 a＝0 时，常称 z 为纯虚数。

什么是虚部

虚部是复数中与实数部分相对应的部分。在复数中，除了实部外，虚部是由虚数单位i构成的。虚数单位i是一个特殊的数，它的特性是i的平方等于-1。虚部通常与实部的运算方式类似，例如相加、相减、相乘和相除等，只是在与实部相乘时虚部会得到一个带有虚数单位的实系数。

虚部是复数中的一部分。在详细解释虚部之前，我们先了解复数的概念。复数是一种数学表达形式，由实数和虚数两部分组成。其中，虚数部分即为虚部。虚数通常表示为“i”，它是复平面上的一个单位向量，并且与实轴垂直。而虚部的定义即为复数中对应虚数部分的值。

虚部也是复数的一个重要组成部分，它涉及到虚数单位i。虚数单位i是一个特殊的数，其特性是i=-1。虚部在复数中用虚数单位i乘以一个实数表示，这部分代表了复数在虚数轴上的投影值。虚部的存在使得复数可以描述一些在实数范围内无法描述的现象，如圆的方程等。

实部指的是一个复数的实数部分，即复数中实数的部分。实部表示复数在实数轴上的投影。虚部指的是一个复数的虚数部分，即复数中虚数的部分。虚部表示复数在虚数轴上的投影。一个复数可以表示为实部加上虚部的形式，例如，对于复数a+bi，a就是实部，b就是虚部。实部和虚部都是实数。

定义：在复数a＋bi中，a称为复数的实部，b称为复数的虚部，i称为虚数单位。当虚部等于零时，这个复数就是实数；当虚部不等于零时，这个复数称为虚数，虚数的实部如果等于零，则称为纯虚数。

虚部是数学名词“复数”中的一个概念，对于复数z=x+iy，其中x，y是任意实数，y称为复数z的虚部，而在笛卡尔直角坐标系中，y轴的值为虚部。利用实部和虚部可以判断两个复数是否相等，定义共轭复数，计算复数的模和辐角主值。