实轴和虚轴是什么（实轴和虚轴是什么图片）

什么是实轴和虚轴,为什么要有实轴和虚轴?

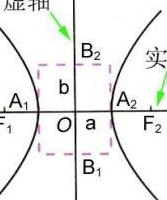
实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如下图所示：线段A1A2叫双曲线的实轴，线段B1B2叫双曲线的虚轴。

答案：实轴和虚轴是复平面坐标系的两个主要组成部分。详细解释：在复平面坐标系中，我们经常遇到复数，它由实部和虚部组成。为了更直观地表示复数，我们引入了复平面坐标系。这个坐标系中的每一条数轴都代表一个特定的数值方向。其中，实轴代表实数部分，虚轴代表虚数部分。

实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如点（1，0），在实轴上取1，虚轴上为0，点位于x轴上，对应复数z=1，虚部为0，为实数。

双曲线与坐标轴两交点的连线段AB叫做实轴。实轴的长度为2a（a为标准方程中的参数）。而虚轴长没有什么实际意义，往往和实轴一起用来讨论渐进线，它的一半就是所谓的表达式中的b。

双曲线的实轴和虚轴分别是什么

1、实轴 两顶点之间的距离称为双曲线的实轴，实轴长的一半称为实半轴。虚轴 在标准方程中令x=0，得y=-b，该方程无实根，为便于作图，在y轴上画出B1（0，b）和B2（0，-b），以B1B2为虚轴。虚轴的一半就叫虚半轴。

2、双曲线的实轴和虚轴分别是。实轴，分为双曲线中的实轴及复数平面中的实轴两类，双曲线中，双曲线与坐标轴两交点的连线段叫实轴。虚轴，一个直角坐标系，纵轴表示纯虚数，为虚轴。

3、双曲线的实轴是指“双曲线与坐标轴两交点的连线段”，而虚轴没有实际意义，它的一半就是所谓的表达式中的b，实轴和虚轴是复数域里的概念，双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。

4、双曲线中实轴等于2a，虚轴等于2b。若为焦点在x轴上的双曲线，在x轴上的两焦点之间的距离长等于2a，也就是是双曲线的实轴，是双曲线两支中相距最近的点，相对应的2b就是虚轴。

5、在双曲线中，实轴等于2a虚轴等于2B 如果是焦点在x轴上的双曲线，那么两个焦点在x轴上的距离等于2a，即双曲线的实轴，即双曲线两个分支之间最近的点，对应的2b为虚轴 实轴长度指的是与定点的距离差为固定长度的常数。其半指的是表达式中所谓的a，而虚轴长度则没有实际意义。

6、实轴 两顶点之间的距离称为双曲线的实轴，实轴长的一半称为实半轴。虚轴 在标准方程中令x=0，得y=-b，该方程无实根，为便于作图，在y轴上画出B1(0，b)和B2(0，-b)，以B1B2为虚轴.如上图中：双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。

实轴和虚轴是什么?

1、实轴和虚轴是复平面坐标系的两个主要组成部分。详细解释：在复平面坐标系中，我们经常遇到复数，它由实部和虚部组成。为了更直观地表示复数，我们引入了复平面坐标系。这个坐标系中的每一条数轴都代表一个特定的数值方向。其中，实轴代表实数部分，虚轴代表虚数部分。

2、实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如点（1，0），在实轴上取1，虚轴上为0，点位于x轴上，对应复数z=1，虚部为0，为实数。

3、实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如下图所示：线段A1A2叫双曲线的实轴，线段B1B2叫双曲线的虚轴。

4、它的一半就是所谓的表达式中的b。实轴和虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标(x，y)构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。 如点(1，0)，在实轴上取1，虚轴上为0，点位于x轴上，对应复数z=1，虚部为0，为实数。

双曲线的实轴和虚轴分别指什么

1、实轴 两顶点之间的距离称为双曲线的实轴，实轴长的一半称为实半轴。虚轴 在标准方程中令x=0，得y=-b，该方程无实根，为便于作图，在y轴上画出B1（0，b）和B2（0，-b），以B1B2为虚轴。虚轴的一半就叫虚半轴。

2、实轴 两顶点之间的距离称为双曲线的实轴，实轴长的一半称为实半轴。虚轴 在标准方程中令x=0，得y=-b，该方程无实根，为便于作图，在y轴上画出B1（0，b）和B2（0，-b），以B1B2为虚轴。

3、双曲线的实轴和虚轴分别是。实轴，分为双曲线中的实轴及复数平面中的实轴两类，双曲线中，双曲线与坐标轴两交点的连线段叫实轴。虚轴，一个直角坐标系，纵轴表示纯虚数，为虚轴。

4、双曲线的实轴是指“双曲线与坐标轴两交点的连线段”，而虚轴没有实际意义，它的一半就是所谓的表达式中的b，实轴和虚轴是复数域里的概念，双曲线是定义为平面交截直角圆锥面的两半的一类圆锥曲线。

5、习惯称X轴为实轴，y轴为虚轴。两顶点之间的线段称为双曲线的实轴，实轴长的一半称为半实轴，实轴的长度为2a（a为标准方程中的参数）。在标准方程中令x=0，得y=-b，该方程无实根，为便于作图，在y轴上画出B1（0，b）和B2（0，-b），以B1B2为虚轴。

实轴和虚轴是什么

实轴和虚轴是复平面坐标系的两个主要组成部分。详细解释：在复平面坐标系中，我们经常遇到复数，它由实部和虚部组成。为了更直观地表示复数，我们引入了复平面坐标系。这个坐标系中的每一条数轴都代表一个特定的数值方向。其中，实轴代表实数部分，虚轴代表虚数部分。

实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如下图所示：线段A1A2叫双曲线的实轴，线段B1B2叫双曲线的虚轴。

实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如点（1，0），在实轴上取1，虚轴上为0，点位于x轴上，对应复数z=1，虚部为0，为实数。

复数实轴和虚轴是什么

实轴虚轴是复数域里的概念，复数z=x+iy，x称为实部，y称为虚部，然后由坐标（x，y）构成的点组成了整个复数域，在坐标平面内，x轴称为实轴，y轴称为虚轴。如点（1，0），在实轴上取1，虚轴上为0，点位于x轴上，对应复数z=1，虚部为0，为实数。

实轴和虚轴是复平面坐标系的两个主要组成部分。详细解释：在复平面坐标系中，我们经常遇到复数，它由实部和虚部组成。为了更直观地表示复数，我们引入了复平面坐标系。这个坐标系中的每一条数轴都代表一个特定的数值方向。其中，实轴代表实数部分，虚轴代表虚数部分。

在复数理论中，实轴与虚轴是关键的几何元素。实轴，即复平面上与x轴相交的线段，其长度由双曲线的标准方程中的参数a决定，通常记为2a。它在复数分析中扮演着基础的角色，与之相对应的是虚轴，它与讨论渐近线时的实轴一起构成对称的坐标轴系统。