共轭转置（共轭转置是什么意思）

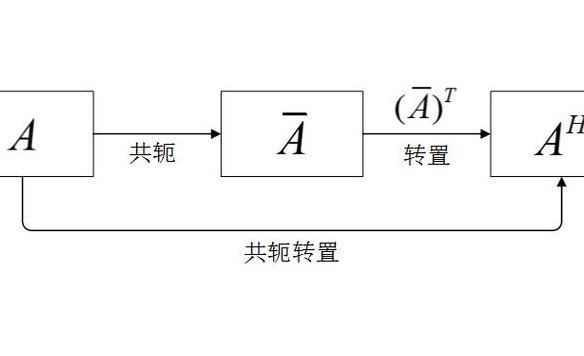
什么是共轭转置矩阵

1、共轭转置就是先取共轭，再取转置。以复数为元素的矩阵，其共轭矩阵指对每一个元素取共轭之后得到的矩阵。共轭矩阵又称Hermite阵，每一个第i行第j列的元素都与第j行第i列的元素的共轭相等。

2、共轭转置，也称为共轭伴随、共轭共轭或共轭转置，是对一个矩阵或向量进行操作的一种方式。对于复数矩阵或向量，其共轭转置将矩阵或向量的每个元素都取复共轭，并将其转置。对于矩阵来说，共轭转置将矩阵的每个元素复共轭，并沿主对角线进行转置。

3、共轭转置矩阵是一个数学术语，指的是将一个矩阵的行列互换，并对每个元素取共轭得到的新的矩阵。接下来，我们将对这个概念进行详细解释。共轭转置矩阵定义 在数学中，矩阵的共轭转置是一种特定的矩阵操作。

4、共轭转置矩阵是一种特定于复数矩阵的操作，它涉及到两个步骤：首先，对矩阵中的每个元素，无论是实数还是虚数，都执行共轭运算，即保持实部不变，将虚部取其负值；接着，进行转置操作，即将矩阵的行与列互换，形成一个对称的矩阵结构。

共轭转置的介绍

1、共轭转置，也称为共轭伴随、共轭共轭或共轭转置，是对一个矩阵或向量进行操作的一种方式。对于复数矩阵或向量，其共轭转置将矩阵或向量的每个元素都取复共轭，并将其转置。对于矩阵来说，共轭转置将矩阵的每个元素复共轭，并沿主对角线进行转置。

2、转置就是把矩阵的每个元素按左上到右下的所有元素对称调换过来。共轭转置就是先取共轭，再取转置。以复数为元素的矩阵，其共轭矩阵指对每一个元素取共轭之后得到的矩阵。共轭矩阵又称Hermite阵，每一个第i行第j列的元素都与第j行第i列的元素的共轭相等。

3、在向量和矩阵的运算中，共轭转置是一个重要的概念。当两个矩阵A和B具有相同的维度时，一个有趣且基本的性质是它们的和的共轭转置等于各部分的共轭转置之和，即(A + B)的共轭转置等于A的共轭转置A*加上B的共轭转置B*。这个性质在矩阵运算中十分实用。

4、共轭转置矩阵是一个数学术语，指的是将一个矩阵的行列互换，并对每个元素取共轭得到的新的矩阵。接下来，我们将对这个概念进行详细解释。共轭转置矩阵定义 在数学中，矩阵的共轭转置是一种特定的矩阵操作。

5、共轭转置是一种矩阵运算，其结果是一个矩阵的转置与其共轭复数的结合。换句话说，共轭转置矩阵是原矩阵的对应元素行转置后取共轭的结果。详细解释如下：共轭转置这个概念涉及两个主要的矩阵运算：转置和取共轭。首先，我们来理解这两个操作。

6、矩阵维数相同，共轭元素变换。矩阵维数相同：进行共轭转置的矩阵A和转置后的矩阵A的维数相同，即都是m乘n型矩阵。共轭元素变换：共轭转置将矩阵A中的每个元素a取共轭得到b，新得到的由b组成的新矩阵记为矩阵B，再对矩阵B作普通转置得到B，即为A的共轭转置矩阵。

共轭转置性质

矩阵维数相同，共轭元素变换。矩阵维数相同：进行共轭转置的矩阵A和转置后的矩阵A的维数相同，即都是m乘n型矩阵。共轭元素变换：共轭转置将矩阵A中的每个元素a取共轭得到b，新得到的由b组成的新矩阵记为矩阵B，再对矩阵B作普通转置得到B，即为A的共轭转置矩阵。

矩阵的共轭转置自身也有特定性质：A的共轭转置的共轭转置仍然是原矩阵，即(A*)* = A。对于方阵A，其行列式和迹的共轭转置也有明确关系：det(A*)等于det A的共轭，且tr(A*)等于tr A的共轭，即det(A*) = (det A)*，tr(A*) = (tr A)*。

在向量和矩阵的运算中，共轭转置是一个重要的概念。当两个矩阵A和B具有相同的维度时，一个有趣且基本的性质是它们的和的共轭转置等于各部分的共轭转置之和，即(A + B)的共轭转置等于A的共轭转置A*加上B的共轭转置B*。这个性质在矩阵运算中十分实用。

共轭转置是什么?

1、共轭转置，也称为共轭伴随、共轭共轭或共轭转置，是对一个矩阵或向量进行操作的一种方式。对于复数矩阵或向量，其共轭转置将矩阵或向量的每个元素都取复共轭，并将其转置。对于矩阵来说，共轭转置将矩阵的每个元素复共轭，并沿主对角线进行转置。

2、共轭转置就是先取共轭，再取转置。以复数为元素的矩阵，其共轭矩阵指对每一个元素取共轭之后得到的矩阵。共轭矩阵又称Hermite阵，每一个第i行第j列的元素都与第j行第i列的元素的共轭相等。

3、共轭转置是一种矩阵运算，其结果是一个矩阵的转置与其共轭复数的结合。换句话说，共轭转置矩阵是原矩阵的对应元素行转置后取共轭的结果。详细解释如下：共轭转置这个概念涉及两个主要的矩阵运算：转置和取共轭。首先，我们来理解这两个操作。

4、在向量和矩阵的运算中，共轭转置是一个重要的概念。当两个矩阵A和B具有相同的维度时，一个有趣且基本的性质是它们的和的共轭转置等于各部分的共轭转置之和，即(A + B)的共轭转置等于A的共轭转置A*加上B的共轭转置B*。这个性质在矩阵运算中十分实用。

5、共轭转置矩阵是一种特定于复数矩阵的操作，它涉及到两个步骤：首先，对矩阵中的每个元素，无论是实数还是虚数，都执行共轭运算，即保持实部不变，将虚部取其负值；接着，进行转置操作，即将矩阵的行与列互换，形成一个对称的矩阵结构。

6、共轭转置矩阵是一个数学术语，指的是将一个矩阵的行列互换，并对每个元素取共轭得到的新的矩阵。接下来，我们将对这个概念进行详细解释。共轭转置矩阵定义 在数学中，矩阵的共轭转置是一种特定的矩阵操作。

a的共轭转置怎么求

1、结论是，对于复数矩阵A，其共轭转置（或称为Hermite转置）可以通过先对矩阵中每个元素取共轭，再将矩阵转置来得到。如果矩阵A和B都是可逆的，那么AB的逆矩阵可以表示为B的逆矩阵乘以A的逆矩阵，即（AB）^-1 = B^-1A^-1。

2、若A，B可逆，则AB可逆，且（AB）^-1=B^-1A^-1。共轭就是矩阵每个元素都取共轭（实部不变，虚部取负）。转置就是把矩阵的每个元素按左上到右下的所有元素对称调换过来。共轭转置就是先取共轭，再取转置。以复数为元素的矩阵，其共轭矩阵指对每一个元素取共轭之后得到的矩阵。

3、在向量和矩阵的运算中，共轭转置是一个重要的概念。当两个矩阵A和B具有相同的维度时，一个有趣且基本的性质是它们的和的共轭转置等于各部分的共轭转置之和，即(A + B)的共轭转置等于A的共轭转置A*加上B的共轭转置B*。这个性质在矩阵运算中十分实用。

4、因此我们可以直接将矩阵A的行和列互换，得到它的转置矩阵。总之，求共轭转置矩阵的方法就是先将原矩阵的行和列互换，得到转置矩阵，然后将转置矩阵中的每个元素都取其共轭复数。这个过程可以用数学公式表示为：C=(AB)^T，其中A是原矩阵，B是转置矩阵，^T表示共轭转置。