内错角相等吗（两线平行内错角相等吗）

两直线平行内错角相等

内错角相等两直线平行。根据平行线的判定定理，两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行。什么情况下两直线平行 同旁内角互补，两直线平行。内错角相等，两直线平行。同位角相等，两直线平行。在同一平面内，垂直于同一条直线的两条直线互相平行。平行于同一条直线的两条直线互相平行。

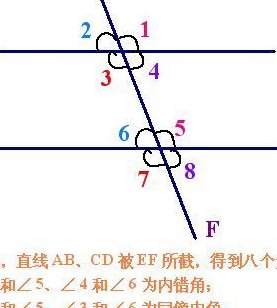
两直线平行内错角相等，这句话是正确的。两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角（alternate angle）。任何一组三线八角都有2对内错角。两条平行直线被第三条直线所截，内错角相等。

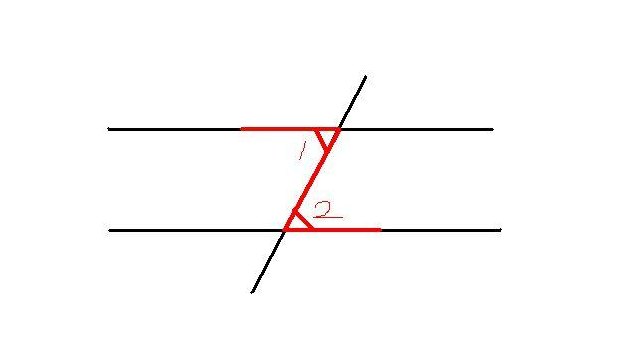
两条直线平行时，内错角相等。这意味着，如果两条直线被第三条直线截断，那么位于两条平行线之间的两对内错角将具有相等的度数。这种现象可以在实际情境中观察到，比如在道路交叉口，当一条直行道路被另一条横穿的道路截断时，从直行道路上的观察者可以看到两对内错角，而这两对角是相等的。

平行线的性质 对平行线的判定而言，两直线平行是结论，而对平行线的性质而言，两直线平行却是条件。已知两直线平行。由平行线得到角的关系是平行线的性质，包括：①两直线平行，同位角相等；②两直线平行，内错角相等；③两直线平行，同旁内角互补。

内错角相等两直线平行是定理。具体解释如下：在欧几里得几何中，这一命题是正确的。我们需要明确内错角的定义：在两条平行线之间，同一侧的内角称为内错角。接下来，我们将通过证明两个内错角相等来证明这两条直线平行。

内错角相等是真命题还是假命题?

1、内错角相等。不是真命题，是假命题。因为掉了一个前提条件，就是两条直线平行，只有在两条直线平行的条件下，内错角才相等。

2、内错角相等是一个假命题。在平面几何中，内错角是位于两条平行线之间，但不在同一直线上的两个角。尽管内错角在平行线之间，但它们不一定相等。例如，考虑两条平行的直线a和b，以及位于这两条直线之间的两个内错角A和B。尽管A和B是内错角，但它们可能不相等。因此，内错角相等是一个假命题。

3、内错角相等不是真命题，而是假命题。两直线平行，内错角相等。才是真命题。两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角。任何一组三线八角都有2对内错角。

4、假命题：内错角相等，只是在两条平行线的前提下才成立。

5、假命题，如果两直线是不平行的，内错角就不相等了啊。同位角，即位置相同，两个角都在第三条直线的同旁，同在被截两条直线的上方或下方。内错角，“内”指在被截两条直线之间；“错”即交错，在第三条直线的两侧。

6、内错角相等为假命题：分析是否为假命题，需要分析题设是否能推出结论，不能推出结论的，即假命题。只有两直线平行，内错角才相等，所以命题“内错角相等”是假命题。

内错角是否相等,为什么

两条平行直线被第三条直线所截，内错角相等。(两直线平行，内错角相等。)若两条不相平行的直线被第三条直线所截，内错角不相等。两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角。

内错角不相等。两条直线被三条直线所截，这样两条直线之内与截线能构成内错角完全取决于两条线段的关系，如果两条线段是任意的两条线段，那么被第三条直线所截，无论有多少组内错角都定不了相等，两条直线必须是平行线这样被第三条直线所截构成的内错角才能相等。

内错角不一定相等，只有当两直线平行时，所形成的内错角才相等。

内错角相等是一个假命题。在平面几何中，内错角是位于两条平行线之间，但不在同一直线上的两个角。尽管内错角在平行线之间，但它们不一定相等。例如，考虑两条平行的直线a和b，以及位于这两条直线之间的两个内错角A和B。尽管A和B是内错角，但它们可能不相等。因此，内错角相等是一个假命题。

无论是同位角还是内错角都可以不相等，同旁内角也可以不互补。因为只有满足两条直线平行的条件时，同位角、内错角才相等，同旁内角才互补。

一对内错角必须相等吗?

1、不一定。如果两直线平行，内错角就相等。同样，内错角相等，两直线平行。

2、内错角一定相等，因为内错角就是指夹在两平行线间的两个角。两条直线被第三条直线所截，两个角分别在截线的两侧，且夹在两条被截直线之间，具有这样位置关系的一对角叫做内错角。任何一组三线八角都有2对内错角。内错角相等，两直线平行。内错角的截取特点是在截线的两旁。

3、内错角不一定相等，只有当两直线平行时，所形成的内错角才相等。