共轭复数怎么求（复数的共轭复数怎么求）

共轭复数是怎么求出来的?

1、已知3+4i，求它的共轭复数：（1）共轭复数，两个实部相等，虚部互为相反数的复数互为共轭复数。当虚部不为零时，共轭复数就是实部相等，虚部相反，如果虚部为零，其共轭复数就是自身（当虚部不等于0时也叫共轭虚数）。（2）实数部分3不变，照写，虚数部分变成4的相反数-4。

2、根据一元二次方程求根公式韦达定理：，当 时，方程无实根，但在复数范围内有2个复根。复根的求法为 （其中 是复数， ）。由于共轭复数的定义是形如 的形式，称 与 为共轭复数。另一种表达方法可用向量法表达： ， 。其中 ，tanΩ=b/a。

3、共轭复数怎么求：用“共轭”概念直接求复数的共轭复数，用“虚部”来求复数的共轭复数，用“共轭角”来求复数的共轭复数。

4、共轭复数的性质 （1）︱x+yi︱=︱x-yi︱；（2）（x+yi）*（x-yi）=x2+y2=︱x+yi︱2=︱x-yi︱2。

5、两个复数的积仍然是一个复数。即：z1z2=（a+bi)(c+di)=ac+adi+bci+bdi2=(ac－bd)+(bc+ad)i。（四）、除法法则：复数除法定义：满足（c+di)(x+yi)=(a+bi）的复数x+yi(x，y∈R）叫复数a+bi除以复数c+di的商运算方法将分子和分母同时乘以分母的共轭复数，再用乘法法则运算。

共轭复数求解答过程

1、已知3+4i，求它的共轭复数：（1）共轭复数，两个实部相等，虚部互为相反数的复数互为共轭复数。当虚部不为零时，共轭复数就是实部相等，虚部相反，如果虚部为零，其共轭复数就是自身（当虚部不等于0时也叫共轭虚数）。（2）实数部分3不变，照写，虚数部分变成4的相反数-4。

2、答案：r1=2+3i，r2=2-3i。解题过程：这道题用配方法更容易明白。

3、取共轭是对复数而言：若 a， b为实数，z=a + bj 为复数，其中：j=√(-1) 为虚数单位；那么复数 z 的共轭为：z* = a - bj ：举例：z = 2+3j。那么z的共轭z*=2-3j z=5-7j，那么z*=5+7j对一个复值函数： z(x)=a(x)+jb(x)，其中a(x)和b(x)都是实值函数。

4、共轭复根是一对特殊根。指多项式或代数方程的一类成对出现的根。若非实复数α是实系数n次方程f(x)=0的根，则其共轭复数α*也是方程f(x)=0的根，且α与α*的重数相同，则称α与α*是该方程的一对共轭复（虚）根。举例：r*r+2r+5=0，求它的共轭复根。

求共轭复数

1、共轭复数的运算公式是Z=a+bi(a，b∈R)，共轭复数，两个实部相等，虚部三为相反数的复 数互为共瓶复数(conjugate cornplex nurmben)。当虚部不为零时，共轭复数就是实部相等，虚部相反，如果虚部为零，其共轭复数就是自身（当虚部不等于0时也叫共轭虚数）。

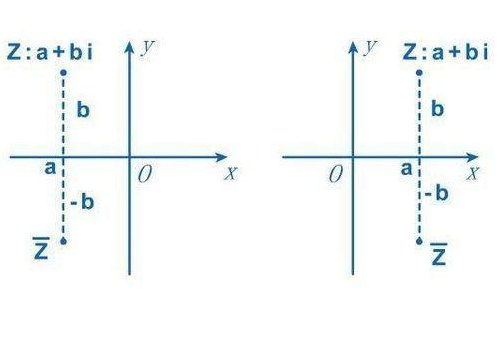
2、共轭复数的定义是若z=a+bi(a，b∈R)，则 z的共轭=a－bi（a，b∈R)。两个实部相等，虚部互为相反数的复数互为共轭复数。两个复数：x+yi与x-yi称为共轭复数，它们的实部相等，虚部互为相反数。在复平面上.表示两个共轭复数的点关于X轴对称。而这一点正是“共轭”一词的来源。

3、当 时，方程无实根，但在复数范围内有2个复根。复根的求法为 （其中 是复数， ）。由于共轭复数的定义是形如 的形式，称 与 为共轭复数。另一种表达方法可用向量法表达： ， 。其中 ，tanΩ=b/a。

4、共轭复数怎么求：用“共轭”概念直接求复数的共轭复数，用“虚部”来求复数的共轭复数，用“共轭角”来求复数的共轭复数。

5、共轭复数的性质 （1）︱x+yi︱=︱x-yi︱；（2）（x+yi）*（x-yi）=x2+y2=︱x+yi︱2=︱x-yi︱2。

6、复数的共轭复数很简单，只要把虚部取反即可，例如：复数5/3+4i的共轭复数是5/3-4i。两个实部相等、虚部互为相反数的复数互为共轭复数。当虚部不为零时，共轭复数就是实部相等，虚部相反；如果虚部为零，其共轭复数就是自身（当虚部不等于0时也叫共轭虚数）。